题目内容
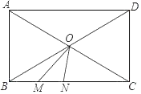
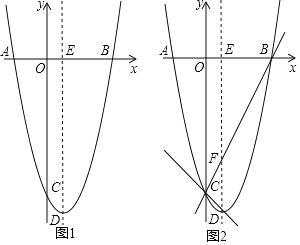
【题目】如图，
是矩形
的边
上一点，以
为折痕翻折，使得点
的对应点落在矩形内部点
处，连接
，若
，
，当
是以
为底的等腰三角形时，
___________．
【答案】
【解析】
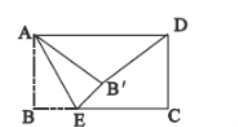
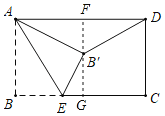
过点B'作B'F⊥AD，延长FB'交BC与点G，可证四边形ABGF是矩形，AF=BG=4，∠BGF=90°，由勾股定理可求B'F=3，可得B'G=2，由勾股定理可求BE的长.
解：如图，过点B'作B'F⊥AD，延长FB'交BC与点G，
∵四边形ABCD是矩形
∴AD=BC=8，∠DAB=∠ABC=90°
∵AB'=B'D，B'F⊥AD
∴AF=FD=4，
∵∠DAB=∠ABC=90°，B'F⊥AD
∴四边形ABGF是矩形
∴AF=BG=4，∠BGF=90°
∵将△ABE以AE为折痕翻折，
∴BE=B'E，AB=AB'=5
在Rt△AB'F中，
∴B'G=2
在Rt△B'EG中，B'E2=EG2+B'G2，
∴BE2=（4-BE）2+4
∴BE=
故答案为：.
练习册系列答案
相关题目
