题目内容
【题目】已知:
分别是
内角和外角平分线．
则
的度数=_ ；
求证:
；
作
，交
延长线于
的延长线交
于
，求证:
．
【答案】（1）90°；（2）见解析；（3）见解析
【解析】
（1）根据角平分线的定义和邻补角的定义即可解得；
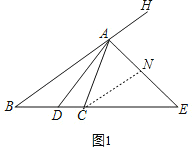
（2）过点C作CN∥AB交AE于点N，如图，易证CA=CN．由CN∥AB可得△ECN∽△EBA，则有
，由CA=CN可得
；
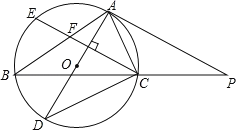
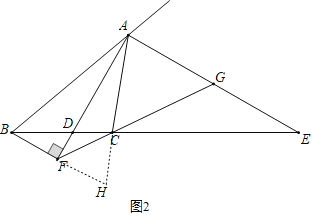
（3）分别延长BF、AC交于点H，证明△ABF≌△AHF，可得BF=HF，证明△BCF∽△ECG，△ACG∽△HCF，可得比例线段，则结论得证．
解：（1）∵AD、AE分别是△ABC中∠A内角的平分线和外角平分线，
∴∠DAE=∠DAC+∠EAC
=
∠BAC+∠CAF
=（∠BAC+∠CAF）
=×180°=90°．
故答案为：90°；
（2）证明：过点
作
交
于点
，如图1，
则有
．
，
，
．
，
，
，
；
（3）如图2，分别延长
、
交于点
；
为
的角平分线，
；
在
与
中，
，
，
；
，
，
，
，
，
，
，
，
∵
，
．
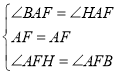练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
