题目内容
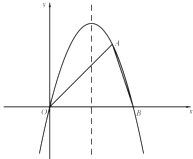
【题目】已知二次函数图象的顶点在原点![]() ,对称轴为
,对称轴为![]() 轴.一次函数
轴.一次函数![]() 的图象与二次函数的图象交于
的图象与二次函数的图象交于![]() 两点(
两点(![]() 在
在![]() 的左侧),且
的左侧),且![]() 点坐标为
点坐标为![]() .平行于
.平行于![]() 轴的直线
轴的直线![]() 过
过![]() 点.
点.
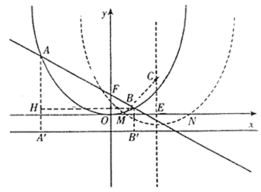
(1)求一次函数与二次函数的解析式;
(2)判断以线段AB为直径的圆与直线![]() 的位置关系,并给出证明;
的位置关系,并给出证明;
(3)把二次函数的图象向右平移 2 个单位,再向下平移 t 个单位(t>0),二次函数的图象与x 轴交于 M,N 两点,一次函数图象交y 轴于 F 点.当 t 为何值时,过 F,M,N 三点的圆的面积最小?最小面积是多少?
【答案】![]() (1)一次函数的解析式为
(1)一次函数的解析式为![]() ;二次函数解析式为
;二次函数解析式为![]() .
.
(2)相切,证明见解析
(3)当![]() 时,过
时,过![]() 三点的圆面积最小,最小面积为
三点的圆面积最小,最小面积为![]() .
.
【解析】
![]() 把
把![]() 代入
代入![]() 得
得![]()
![]() 一次函数的解析式为
一次函数的解析式为![]()
![]() 二次函数图象的顶点在原点,对称轴为
二次函数图象的顶点在原点,对称轴为![]() 轴,
轴,
![]() 二次函数的解析式为
二次函数的解析式为![]() ,将
,将![]() 代入解析式得
代入解析式得![]()
![]() 二次函数的解析式为
二次函数的解析式为![]()
![]() 由
由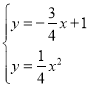 解得
解得![]() 或
或![]() ,
,![]() ,取
,取![]() 的中点
的中点![]() ,
,
过![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,则
,则![]()
![]() ,而直径
,而直径
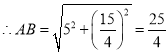
![]() ,即圓心到直线
,即圓心到直线![]() 的距离等于半径,
的距离等于半径,
以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切.
相切.
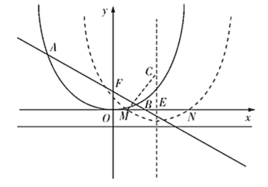
![]() 平移后二次函数的解析式为
平移后二次函数的解析式为![]() ,
,
令![]() 得
得![]()
![]() 过
过![]() 三点的國的圆心
三点的國的圆心![]() 一定在平移后抛物线的对称轴.上,要使圓面积最小,圆半径应等于点
一定在平移后抛物线的对称轴.上,要使圓面积最小,圆半径应等于点![]() 到直线
到直线![]() 2的距离,点
2的距离,点![]() 坐标为
坐标为![]() .
.
此时,半径为![]() ,面积为
,面积为![]()
设圆心为![]() 的中点为
的中点为![]() ,连接
,连接![]() ,则
,则![]() ,
,
在三角形![]() 中,
中,![]()
![]() ,而
,而![]()
![]() 当
当![]() 时,过
时,过![]() 三点的圓面积最小,最小面积为
三点的圓面积最小,最小面积为![]() .
.

练习册系列答案
相关题目
【题目】某射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对他们进行了8次测试,测试成绩(单位:环)如下表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 | 第八次 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 | 10 | 8 |
乙 | 10 | 7 | 10 | 10 | 9 | 8 | 8 | 10 |
(1)根据表格中的数据,计算出甲的平均成绩是 环,乙的平均成绩是 环;
(2)分别计算甲、乙两名运动员8次测试成绩的方差;
(3)根据(1)(2)计算的结果,你认为推荐谁参加全国比赛更合适,并说明理由.