题目内容
【题目】如图,矩形OABC的两边落在坐标轴上,反比例函数y=![]() 的图象在第一象限的分支过AB的中点D交OB于点E,连接EC,若△OEC的面积为12,则k=_____.
的图象在第一象限的分支过AB的中点D交OB于点E,连接EC,若△OEC的面积为12,则k=_____.

【答案】12![]() .
.
【解析】
设AD=a,则AB=OC=2a,根据点D在反比例函数y=![]() 的图象上,可得D点的坐标为(a,
的图象上,可得D点的坐标为(a,![]() ),所以OA=
),所以OA=![]() ;过点E 作EN⊥OC于点N,交AB于点M,则OA=MN=
;过点E 作EN⊥OC于点N,交AB于点M,则OA=MN=![]() ,已知△OEC的面积为12,OC=2a,根据三角形的面积公式求得EN=
,已知△OEC的面积为12,OC=2a,根据三角形的面积公式求得EN=![]() ,即可求得EM=
,即可求得EM=![]() ;设ON=x,则NC=BM=2a-x,证明△BME∽△ONE,根据相似三角形的性质求得x=
;设ON=x,则NC=BM=2a-x,证明△BME∽△ONE,根据相似三角形的性质求得x=![]() ,即可得点E的坐标为(
,即可得点E的坐标为(![]() ,
,![]() ),根据点E在在反比例函数y=
),根据点E在在反比例函数y=![]() 的图象上,可得
的图象上,可得![]() ·
·![]() =k,解方程求得k值即可.
=k,解方程求得k值即可.
设AD=a,则AB=OC=2a,
∵点D在反比例函数y=![]() 的图象上,
的图象上,
∴D(a,![]() ),
),
∴OA=![]() ,
,
过点E 作EN⊥OC于点N,交AB于点M,则OA=MN=![]() ,
,
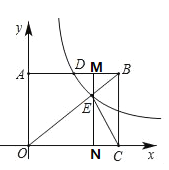
∵△OEC的面积为12,OC=2a,
∴EN=![]() ,
,
∴EM=MN-EN=![]() -
-![]() =
=![]() ;
;
设ON=x,则NC=BM=2a-x,
∵AB∥OC,
∴△BME∽△ONE,
∴![]() ,
,
即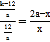 ,
,
解得x=![]() ,
,
∴E(![]() ,
,![]() ),
),
∵点E在在反比例函数y=![]() 的图象上,
的图象上,
∴![]() ·
·![]() =k,
=k,
解得k=![]() ,
,
∵k>0,
∴k=12![]() .
.
故答案为:12![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目