Question

【题目】如图，在平面直角坐标系中，一次函数的图像分别交x、y轴于点A,B，与一次函数y=kx的图像交于第一象限内的点C．

（1）当∠时，求点C的坐标。

（2）当时，求k的值。

Answer 1

【答案】（1）点C的坐标为（4，4）；（2）.

【解析】

（1）如图1，过C作CD⊥OB于D，根据∠COB＝45°可得OD＝CD，设C点坐标为：（a，a），代入一次函数求出a即可；

（2）如图2，过C作CE⊥OA于E，根据一次函数解析式求出OB和OA，然后根据等腰三角形的判定和性质以及三角形中位线定理求出OE和CE，得到C点坐标即可求出k值．

解：（1）如图1，过C作CD⊥OB于D，

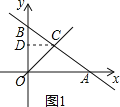
∵∠COB＝45°，

∴OD＝CD，

设C点坐标为：（a，a），代入，可得，

解得：，

即点C的坐标为（4，4）；

（2）如图2，过C作CE⊥OA于E，

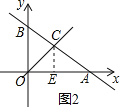
在一次函数中，令x＝0，解得y＝6，令y＝0，解得x＝12，

∴B点的坐标为（0，6），A点的坐标为（12，0），

即OB=6，OA=12，

∵，

∴CO=CA，

∴E是OA中点，

∴OE=OA=6，

∵CE∥OB，

∴CE=OB=3，

∴C（6，3），

将（6，3）代入y=kx得：3=6k，

∴.