题目内容
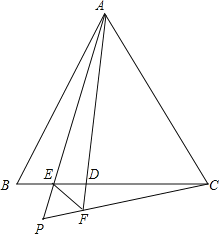
【题目】如图,把一张长方形的纸片ABCD沿BD对折,使C点落在E点处,BE与AD相交于点O。
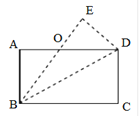
(1)由折叠可知△BCD≌△BED,除此之外,图中还存在其他的全等三角形,请写出其他一组全等三角形__________________.
(2)图中有等腰三角形吗?请你找出来__________________.
(3)若AB=6,BC=8,求OB的长度。
【答案】(1)△ABD≌△CDB,△ABD≌△EDB,△EOD≌△AOB(任意写出一组即可).(2)△BOD;(3)![]() .
.
【解析】
(1)根据矩形的性质可得:△ABD≌△CDB,那么△ABD≌△EDB;而AB=CD=DE,且∠A、∠E都是直角,由此可证得△EOD≌△AOB,因此图中除了△BCD≌△BED外共有3对全等三角形,任意写出一组即可;
(2)根据△EOD≌△AOB,故得到BO=DO,得到△BOD为等腰三角形;
(3)设OB为x,则DO=x,AO=8-x,再根据Rt△AOB,利用勾股定理即可列方程求解.
(1)共有3对全等三角形:△BED≌△CDB,△ABD≌△EDB,△EOD≌△AOB(任意写出一组即可);
以△EOD≌△AOB为例进行说明:
由折叠的性质知:CD=DE=AB,∠E=∠C=∠A=90°;
在△EOD和△AOB中,
∴△EOD≌△AOB(AAS);
故答案为:△ABD≌△CDB,△ABD≌△EDB,△EOD≌△AOB(任意写出一组即可).
(2)∵△EOD≌△AOB,∴BO=DO,故△BOD为等腰三角形;
故填:△BOD;
(3)设OB为x,则DO=x,AO=8-x,
在Rt△AOB,![]()
即![]()
解得x=![]()
故OB=![]() .
.


练习册系列答案
相关题目