题目内容
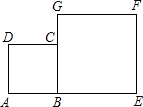
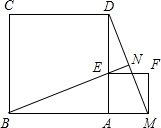
如图,正方形ABCD的边长为1,点P为BC边上的任意一点(可与点B或C重合),分别过B、D作AP的垂线段,垂足分别是B1、D1.猜想:(DD1)2+(BB1)2的值,并对你的猜想加以证明.


猜想:(DD1)2+(BB1)2的值是1;
证明如下:在△ADD1和△ABB1中
∵四边形ABCD是正方形,
∴AD=AB,
∵AD1⊥DD1,BB1⊥AB1,
∴∠DD1A=∠AB1B=90°,
∵∠DAD1+∠B1AB=∠B1AB+∠ABB1,
∴∠DAD1=∠ABB1,
∴△ADD1≌△BAB1,
∴AD1=BB1,
∵(DD1)2+(BB1)2=(DD1)2+(AD1)2=AD2=1,
∴(DD1)2+(BB1)2=1;

证明如下:在△ADD1和△ABB1中
∵四边形ABCD是正方形,
∴AD=AB,
∵AD1⊥DD1,BB1⊥AB1,
∴∠DD1A=∠AB1B=90°,
∵∠DAD1+∠B1AB=∠B1AB+∠ABB1,
∴∠DAD1=∠ABB1,
∴△ADD1≌△BAB1,
∴AD1=BB1,
∵(DD1)2+(BB1)2=(DD1)2+(AD1)2=AD2=1,
∴(DD1)2+(BB1)2=1;


练习册系列答案
相关题目