Question

【题目】定义：我们知道，四边形的一条对角线把这个四边形分成了两个三角形，如果这两个三角形相似（不全等），我们就把这条对角线叫做这个四边形的“相似对角线”；

理解：

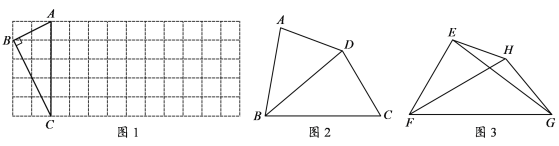
⑴ 如图1，△ABC的三个顶点均在正方形网格中的格点上，若四边形ABCD是以AC为“相似对角线”的四边形，请用无刻度的直尺在网格中画出点D（保留画图痕迹，找出3个即可）；

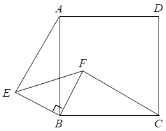
⑵ 如图2，在四边形ABCD中，∠ABC＝80°，∠ADC＝140°，对角线BD平分∠ABC. 请问BD是四边形ABCD的“相似对角线”吗？请说明理由；

运用：

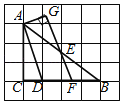
⑶ 如图3，已知FH是四边形EFGH的“相似对角线”， ∠EFH＝∠HFG＝30°.连接EG，若△EFG的面积为，求FH 的长.

Answer 1

【答案】（1）如图1，△ACD1、△ACD2、、△ACD3、△ACD4（任画三个即可）；（2）BD是四边形ABCD的“相似对角线”，理由见解析；（3）FH=．

【解析】

（1）根据“相似对角线”的定义，利用方格纸的特点可找到D点的位置；

（2）先说明∠A+∠ADB=140°=∠ADC，即可说明理由；

（3）先判断出△FEHC∽△FHG，得出FH2=FE·FG，再求出EQ=FE，即可求得FH的值．

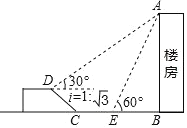
解：（1）由图1可得，AB=，BC=2，∠ABC=90°，AC=5，

四边形ABCD是以AC为“相似对角线”的四边形，

①当∠ACD=90°时，△ACD∽△ABC或△ACD∽△CBA，

∴或

∴CD=10或CD=2.5

同理：当∠CAD=90°时，AD=2.5或AD=10．

根据方格纸的特点可找到D点的位置，然后再连接CD或AD

即如图△ACD1、△ACD2、、△ACD3、△ACD4（任画三个即可）即为所求；

（2）BD是四边形ABCD的“相似对角线”，理由如下：

∵∠ABC=80°，BD平分∠ABC，

∴∠ABD=∠DBC=40°，

∵∠A+∠ADB=140°

∵∠ADC=140°，

∴∠BDC+∠ADB=140°，

∴∠A=∠BDC，

∴△ABD∽△DBC，

∴BD是四边形ABCD的“相似对角线”；

（3）∵FH是四边形EFGH的“相似对角线”，

∴△EFH与△HFG相似，

∵∠EFH=∠HFG，

∴△FEHC∽△FHG，

∴

∴FH2=FE·FG，

如图3，过点E作EQ⊥FG于Q，

∴EQ=FE·sin60°=FE，

∵.

∴

∴FG·FE=24，

∵FH2=FE·FG，

∴FH2=24

∴FH=，FH=-（舍去）