题目内容
已知:如图,在平面直角坐标系xoy中,一次函数y=
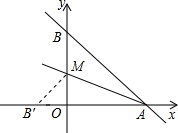
x+3的图象与x轴和y轴交于A、B 两点,将△AOB绕点O顺时针旋转90°后得到△A′OB′.
两点,将△AOB绕点O顺时针旋转90°后得到△A′OB′.
(1)求直线A′B′的解析式;
(2)若直线A′B′与直线AB相交于点C,求S△A?BC:S△ABO的值.
| 3 |
| 4 |
 两点,将△AOB绕点O顺时针旋转90°后得到△A′OB′.
两点,将△AOB绕点O顺时针旋转90°后得到△A′OB′.(1)求直线A′B′的解析式;
(2)若直线A′B′与直线AB相交于点C,求S△A?BC:S△ABO的值.
(1)根据y=
x+3,解得点坐标A(-4,0),B(0,3),即OA=4,OB=3,
∴OA′=OA=4,OB′=OB=3,
∴A′(0,4),B′(3,0),
设直线A′B′的解析式为y=kx+b,则
,解得
,
∴直线A′B′的解析式为y=-
+4;
(2)解方程组
,
求得两直线交点坐标,得C(
,
),
∴S△A′BC=1×
×
=
,S△ABO=4×3×
=6,
∴
=
.
| 3 |
| 4 |
∴OA′=OA=4,OB′=OB=3,
∴A′(0,4),B′(3,0),
设直线A′B′的解析式为y=kx+b,则
|
|
∴直线A′B′的解析式为y=-
| 4x |
| 3 |
(2)解方程组
|
求得两直线交点坐标,得C(
| 12 |
| 25 |
| 84 |
| 25 |
∴S△A′BC=1×
| 12 |
| 25 |
| 1 |
| 2 |
| 6 |
| 25 |
| 1 |
| 2 |
∴
| S△A′BC |
| S△ABO |
| 1 |
| 25 |

练习册系列答案
相关题目
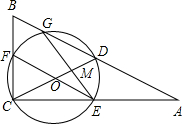
 (OA>OB),动点P从O点出发,沿路线O?B?A以每秒1个单位长度的速度运动,到达A点时运动停止.
(OA>OB),动点P从O点出发,沿路线O?B?A以每秒1个单位长度的速度运动,到达A点时运动停止. 距甲地的距离为y米,y与x的函数图象如图所示.根据图象信息,解答下列问题:
距甲地的距离为y米,y与x的函数图象如图所示.根据图象信息,解答下列问题: