题目内容
直线y=1.5x-3分别交x,y轴于A、B两点,O是原点.
(1)求出A、B两点的坐标;
(2)求△AOB的面积;
(3)过△AOB的顶点能不能画出直线把△AOB分成面积相等的两部分?若能,可以画出几条?请任选一条求出该直线所对应的函数关系式.
(1)求出A、B两点的坐标;
(2)求△AOB的面积;
(3)过△AOB的顶点能不能画出直线把△AOB分成面积相等的两部分?若能,可以画出几条?请任选一条求出该直线所对应的函数关系式.
(1)∵令y=0,则x=2;
令x=0,则y=-3,
∴A(2,0),B(0,-3);
(2)∵由(1)知,A(2,0),B(0,-3),
∴OA=2,OB=3,
∴S△OAB=
OA•OB=
×2×3=3;
(3)∵同底等高的三角形面积相等,
∴△AOB的任一顶点与对边中点的连线把三角形分成面积相等的两部分,
∴可以画出3条;
如图所示,若D为线段AB的中点,则直线OD把△AOB分成面积相等的两部分,
∵A(2,0),B(0,-3),D为线段AB的中点,
∴D(1,-
),
设直线OD的解析式为y=kx(k≠0),则-
=k,
∴直线OD的解析式为y=-
x.
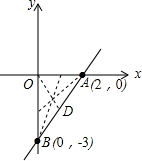
令x=0,则y=-3,
∴A(2,0),B(0,-3);
(2)∵由(1)知,A(2,0),B(0,-3),
∴OA=2,OB=3,
∴S△OAB=
| 1 |
| 2 |
| 1 |
| 2 |
(3)∵同底等高的三角形面积相等,
∴△AOB的任一顶点与对边中点的连线把三角形分成面积相等的两部分,
∴可以画出3条;
如图所示,若D为线段AB的中点,则直线OD把△AOB分成面积相等的两部分,
∵A(2,0),B(0,-3),D为线段AB的中点,
∴D(1,-
| 3 |
| 2 |
设直线OD的解析式为y=kx(k≠0),则-
| 3 |
| 2 |
∴直线OD的解析式为y=-
| 3 |
| 2 |
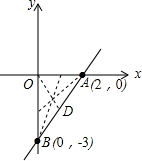

练习册系列答案
相关题目

 两点,将△AOB绕点O顺时针旋转90°后得到△A′OB′.
两点,将△AOB绕点O顺时针旋转90°后得到△A′OB′.





