题目内容
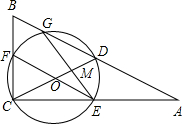
如图,在△ABC中∠ACB=90°,D是AB的中点,以DC为直径的⊙O交△ABC的三边,交点分别是G,F,E点.GE,CD的交点为M,且ME=4
,MD:CO=2:5.
(1)求证:∠GEF=∠A;
(2)求⊙O的直径CD的长;
(3)若cos∠B=0.6,以C为坐标原点,CA,CB所在的直线分别为X轴和Y轴,建立平面直角坐标系,求直线AB的函数表达式.
| 6 |
(1)求证:∠GEF=∠A;
(2)求⊙O的直径CD的长;
(3)若cos∠B=0.6,以C为坐标原点,CA,CB所在的直线分别为X轴和Y轴,建立平面直角坐标系,求直线AB的函数表达式.

(1)证明:连接DF,
∵CD是圆直径∴∠CFD=90°即DF⊥BC,
∵∠ACB=90°,∴DF∥AC,
∴∠BDF=∠A,
∵在⊙O中∠BDF=∠GEF,∴∠GEF=∠A.
(2)∵D是Rt△ABC斜边AB的中点,
∴DC=DA,
∴∠DCA=∠A,
又由(1)知∠GEF=∠A∴∠DCA=∠GEF,
又∵∠OME=∠EMC,
∴△OME∽△EMC相似,
∴
=
∴ME2=OM×MC,
又∵ME=4
∴OM×MC=(4
)2=96,
∵MD:CO=2:5,
∴OM:MD=3:2,∴OM:MC=3:8,
设OM=3xMC=8x,
∴3x×8x=96,
∴x=2,
直径CD=10x=20.
(3)∵Rt△ABC斜边AB的中线CD=20,
∴AB=40,
∵在Rt△ABC中,cos∠B=0.6=
,∴BC=24,
∴AC=32,
设直线AB的函数表达式为y=kx+b根据题意得A(32,0)B(0,24),
b=24,0×k+b=24解得k=-
,32×k+b=0,
∴直线AB的函数解析式为y=-
x+24.

∵CD是圆直径∴∠CFD=90°即DF⊥BC,
∵∠ACB=90°,∴DF∥AC,
∴∠BDF=∠A,
∵在⊙O中∠BDF=∠GEF,∴∠GEF=∠A.
(2)∵D是Rt△ABC斜边AB的中点,
∴DC=DA,
∴∠DCA=∠A,
又由(1)知∠GEF=∠A∴∠DCA=∠GEF,
又∵∠OME=∠EMC,
∴△OME∽△EMC相似,
∴
| OM |
| ME |
| ME |
| MC |
又∵ME=4
| 6 |
| 6 |
∵MD:CO=2:5,
∴OM:MD=3:2,∴OM:MC=3:8,
设OM=3xMC=8x,
∴3x×8x=96,
∴x=2,
直径CD=10x=20.
(3)∵Rt△ABC斜边AB的中线CD=20,
∴AB=40,
∵在Rt△ABC中,cos∠B=0.6=
| BC |
| AB |
∴AC=32,
设直线AB的函数表达式为y=kx+b根据题意得A(32,0)B(0,24),
b=24,0×k+b=24解得k=-
| 3 |
| 4 |
∴直线AB的函数解析式为y=-
| 3 |
| 4 |


练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
 两点,将△AOB绕点O顺时针旋转90°后得到△A′OB′.
两点,将△AOB绕点O顺时针旋转90°后得到△A′OB′.





 已知油箱中的余油量y(升)与行驶时间t(小时)的关系如下表,
已知油箱中的余油量y(升)与行驶时间t(小时)的关系如下表,