题目内容
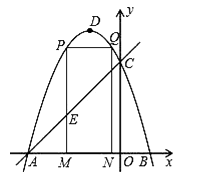
【题目】如图,已知△ABC的面积为16,BC=8,现将△ABC沿直线向右平移a(a<8)个单位到△DEF的位置.

(1)求△ABC的BC边上的高.
(2)连结AE、AD,设AB=5
①求线段DF的长.
②当△ADE是等腰三角形时,求a的值.
【答案】(1)4;(2)①![]() ;②
;②![]() 或5或6
或5或6
【解析】
(1)根据三角形的面积公式即可求出结论;
(2)①作AG⊥BC,垂足为G,根据勾股定理即可求出BG,再根据勾股定理即可求出AC,最后根据平移的性质即可求出结论;
②根据等腰三角形腰的情况分类讨论,根据平移的性质、勾股定理和等腰三角形的性质分别求出结论即可.
解:(1)△ABC的BC边上的高为16×2÷8=4
(2)①作AG⊥BC,垂足为G,由(1)知AG=4

在Rt△AGB中,AB=5,AG=4
![]() 3
3
在Rt△AGC中,AG=4,GC=BC-BG=5
![]()
由平移可得DF=AC=![]()
②若△ADE是等腰三角形,可分以下情况
Ⅰ、当AD=AE时,由题可得:AD=BE=a=AE

在Rt△AGE中,EG=a-3
根据勾股定理可得:
![]()
解得:![]()
Ⅱ、当AD=DE时,由平移可得DE=AB=5
∴a=AD=DE=5
Ⅲ、当DE=AE时,则AB=AE

∵AG⊥BC
∴BE=2BG=6
即a=6
综上可得:当a=![]() 或5或6时,△ADE是等腰三角形
或5或6时,△ADE是等腰三角形

【题目】谁更合理?
某种牙膏上部圆的直径为2.6cm,下部底边的长为4cm,如图,现要制作长方体的牙膏盒,牙膏盒底面是正方形,在手工课上,小明、小亮、小丽、小芳制作的牙膏盒的高度都一样,且高度符合要求.不同的是底面正方形的边长,他们制作的边长如下表:
制作者 | 小明 | 小亮 | 小丽 | 小芳 |
正方形的边长 | 2cm | 2.6cm | 3cm | 3.4cm |
(1)这4位同学制作的盒子都能装下这种牙膏吗?(![]() )
)
(2)若你是牙膏厂的厂长,从节约材料又方便取放牙膏的角度来看,你认为谁的制作更合理?并说明理由.