题目内容
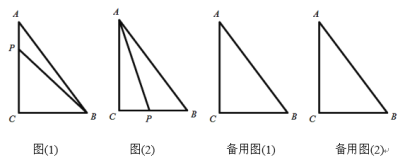
【题目】如图,BF,CG分别是![]() 的高线,点D,E分别是BC,GF的中点,连结DF,DG,DE,
的高线,点D,E分别是BC,GF的中点,连结DF,DG,DE,
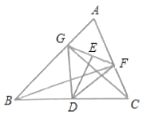
(1)求证:![]() 是等腰三角形.
是等腰三角形.
(2)若![]() ,求DE的长.
,求DE的长.
【答案】(1)证明见详解;(2)4.
【解析】
(1)由BF,CG分别是![]() 的高线,点D是BC的中点,可得:DG=
的高线,点D是BC的中点,可得:DG=![]() BC,DF=
BC,DF=![]() BC,进而得到结论;
BC,进而得到结论;
(2)由![]() 是等腰三角形,点E是FG的中点,可得DE垂直平分FG,然后利用勾股定理,即可求解.
是等腰三角形,点E是FG的中点,可得DE垂直平分FG,然后利用勾股定理,即可求解.
(1)∵BF,CG分别是![]() 的高线,
的高线,
∴CG⊥AB,BF⊥AC,
∴△BCG和△BCF是直角三角形,
∵点D是BC的中点,
∴DG=![]() BC,DF=
BC,DF=![]() BC,
BC,
∴DG=DF,
∴![]() 是等腰三角形;
是等腰三角形;
(2)∵BC=10,
∴DF=![]() BC=
BC=![]() ×10=5,
×10=5,
∵![]() 是等腰三角形,点E是GF的中点,
是等腰三角形,点E是GF的中点,
∴DE⊥GF,EF=![]() GF=
GF=![]() ×6=3,
×6=3,
∴![]() .
.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目