题目内容
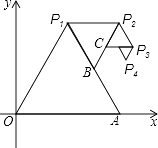
【题目】直线![]() 经过原点和点
经过原点和点![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(1)求直线![]() 所对应的函数解析式;
所对应的函数解析式;
(2)当P在线段OA上时,设![]() 点横坐标为
点横坐标为![]() ,三角形
,三角形![]() 的面积为
的面积为![]() ,写出
,写出![]() 关于
关于![]() 的函数解析式,并指出自变量
的函数解析式,并指出自变量![]() 的取值范围;
的取值范围;
(3)当P在射线OA上时,在坐标轴上有一点![]() ,使
,使![]() (
(![]() 正整数),请直接写出点
正整数),请直接写出点![]() 的坐标(本小题只要写出结果,不需要写出解题过程)
的坐标(本小题只要写出结果,不需要写出解题过程)

【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)利用待定系数法即可解决问题;
(2)利用三角形的面积公式计算即可;
(3)分两种情形分别求解即可.
(1)设直线l的解析式为y=kx,
把点A坐标代入得到6=3k,
∴k=2,
∴直线l的解析式为y=2x.
(2)∵P(x,2x),B(4,0),
∴S=![]() ×4×2x=4x,(0<x≤3);
×4×2x=4x,(0<x≤3);
(3)∵点B的坐标为(6,0),点C在坐标轴上,
①当点C在x轴上时,则△BOP和△COP是同高三角形,
∵S△BOP:S△COP=2:m,
∴![]() ,
,
∴OC=3m,
∴C(3m,0)或(-3m,0);
②当点C在x轴上时,则△BOP和△COP是同高三角形,
∵P(x,2x),S△BOP:S△COP=2:m,
∴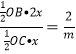 ,即
,即![]() ,
,
∴OC=6m,
∴C(0,6m)或(0,-6m).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目