题目内容
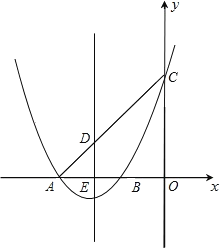
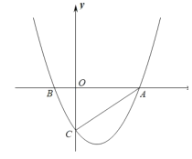
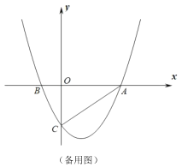
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,连接
点,连接![]() ,已知
,已知![]() ,且抛物线经过点
,且抛物线经过点![]() .
.
(1)求抛物线的解析式;
(2)若点![]() 是抛物线上位于
是抛物线上位于![]() 轴下方的一点,且
轴下方的一点,且![]() ,求
,求![]() 的坐标;
的坐标;
(3)若点![]() 是
是![]() 轴上一点,以
轴上一点,以![]() 三点为顶点的三角形是等腰三角形,求
三点为顶点的三角形是等腰三角形,求![]() 点的坐标.
点的坐标.
【答案】(1)![]() ;(2)
;(2)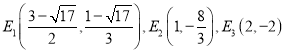 ;(3)
;(3)![]() ,
,![]() ,
,![]() ,
,![]()
【解析】
(1)将点B,D的坐标分别代入抛物线的解析式,建立关于a,c的方程组,解方程组求出a,c的值,就可得到抛物线的解析式.(2)由y=0,求出对应的x的值,即可得到点A的坐标,从而可求出AB的长,再由x=0求出对应的y的值,可得到点C的坐标,然后利用三角形的面积公式求出△ABC的面积,利用待定系数法求出直线AC的函数解析式,过点E作x轴的垂线交lAC于点F,利用函数解析式设点F,E的坐标,利用已知条件建立关于a的方程,解方程求出a的值,即可得到符合题意的点E的坐标.(3)利用等腰三角形的判定,分情况讨论:当点A为等腰△PAC的顶点时,AC=AP;当点C为等腰△PAC的顶点时,CA=CP;当点P为等腰△PAC的顶点时,CA=CP, 分别求出符合题意的点P的坐标.
(1)将点![]() ,点
,点![]() 代入
代入![]() ,
,
可得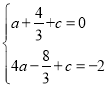 ,解得
,解得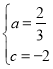 ,
,
![]() 抛物线解析式:
抛物线解析式:![]() ;
;
(2)当![]() 时,
时,![]() ,
,
解方程![]() ,得
,得![]() ,
,
![]() ,
,
![]() ,
,
当![]() 时,
时,![]() ,
,
![]() ,
,
![]() ,
,
设![]() ,将点
,将点![]() 代入
代入![]() ,
,
得![]() ,解得
,解得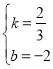 ,
,
![]() ,
,
如图1,过点![]() 作
作![]() 轴的垂线交
轴的垂线交![]() 于点
于点![]() ,
,
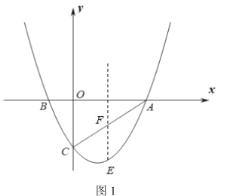
设点![]() ,点
,点![]() ,其中
,其中![]() ,
,
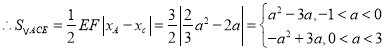 ,
,
由![]() ,
,
可得![]() 或
或![]() ,
,
解得:![]() (舍),
(舍),![]() ,
,
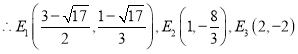 ;
;
(3)情形一:当点![]() 为等腰
为等腰![]() 的顶点时,
的顶点时,![]() ,如图2,
,如图2,
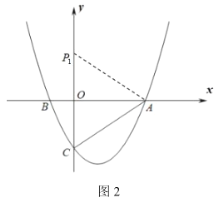
![]() ,
,
![]() ,
,
![]() 点
点![]() ;
;
情形二:当点![]() 为等腰
为等腰![]() 的顶点时,
的顶点时,![]() ,如图3,
,如图3,
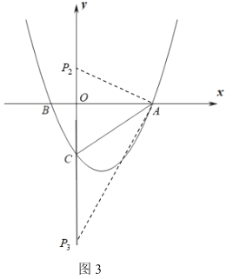
![]() ,
,
![]() ;
;
情形三:当点![]() 为等腰
为等腰![]() 的顶点时,
的顶点时,![]() ,如图4,
,如图4,
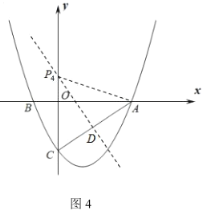
过线段![]() 的中点
的中点![]() 作垂线交
作垂线交![]() 轴于点
轴于点![]() ,
,
由中点坐标公式可得![]() ,
,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
当![]() 时,
时,![]() ,
,
![]() ;
;
综上所述:![]() ,
,![]() ,
,![]() ,
,![]() .
.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目