题目内容
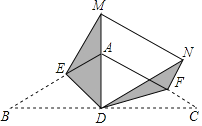
【题目】如图,![]() 的顶点
的顶点![]() 在抛物线
在抛物线![]() 上,将
上,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,现将抛物线沿
,现将抛物线沿![]() 轴向上平移
轴向上平移![]() 个单位,使得抛物线与边
个单位,使得抛物线与边![]() 只有一个公共点
只有一个公共点![]() ,则
,则![]() 的取值范围为__________.
的取值范围为__________.
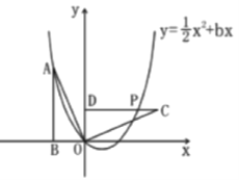
【答案】![]() 或
或![]()
【解析】
把点A(-2,4)代入![]() 求得
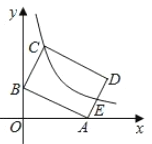
求得![]() ,利用旋转的性质求得点C(4,2),点D(0,2),观察图象,将抛物线沿y轴向上平移2个单位,经过点D时与线段CD恰好有二个交点,求得
,利用旋转的性质求得点C(4,2),点D(0,2),观察图象,将抛物线沿y轴向上平移2个单位,经过点D时与线段CD恰好有二个交点,求得![]() ,当顶点在线段CD上时,可求得m的值即可求解.
,当顶点在线段CD上时,可求得m的值即可求解.
把点A(-2,4)代入![]() 得:
得:![]() ,
,
解得:![]() ,
,
∴抛物线的解析式为:![]() ,
,
∵点A(-2,4),
∴OB=2,AB=4,
根据旋转的性质知:OD=OB=2,CD=AB=4,如图:
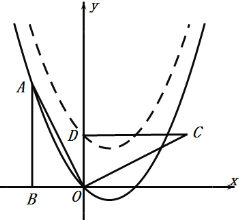
∴点C的坐标为(4,2),点D的坐标为(0,2),
设抛物线沿y轴向上平移![]() 个单位的解析式为
个单位的解析式为![]() ,
,
当![]() 时,
时,![]() ,
,
此时抛物线![]() 与线段CD只有一个交点,
与线段CD只有一个交点,
将抛物线沿y轴向上平移2个单位,经过点D时与线段CD恰好有二个交点,
∴![]() ,抛物线
,抛物线![]() 与线段CD只有一个交点,
与线段CD只有一个交点,
当抛物线![]() 顶点在线段CD上时,抛物线
顶点在线段CD上时,抛物线![]() 与线段CD只有一个交点,
与线段CD只有一个交点,
此时: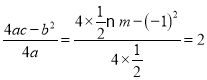 ,解得:
,解得:![]() ,
,
故答案为:![]() 或
或![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目