题目内容
【题目】在平面直角坐标系![]() 中,函数
中,函数![]() (
(![]() )的图象G与直线
)的图象G与直线![]() 交于点A(4,1),点B(1,n)(n≥4,n为整数)在直线l上.
交于点A(4,1),点B(1,n)(n≥4,n为整数)在直线l上.
(1)求![]() 的值;
的值;
(2)横、纵坐标都是整数的点叫做整点.记图象![]() 与直线l围成的区域(不含边界)为W.
与直线l围成的区域(不含边界)为W.
①当n=5时,求![]() 的值,并写出区域W内的整点个数;
的值,并写出区域W内的整点个数;
②若区域W内恰有5个整点,结合函数图象,求![]() 的取值范围.
的取值范围.
【答案】(1)m=4;(2)①区域![]() 内有2个整点;②
内有2个整点;②![]()
【解析】
(1)把点A的坐标代入反比例函数解析式求解即可;
(2)①先求出当n=5时![]() 的值,然后结合函数图象解答即可;
的值,然后结合函数图象解答即可;
②如图2,分别求出当n=6、n=7时k的值,再结合函数图象求出区域![]() 内的整点个数,进而可判断当n≥8时区域
内的整点个数,进而可判断当n≥8时区域![]() 内的整点个数,从而可得结果.
内的整点个数,从而可得结果.
解:(1)∵点A(4,1)在函数![]() (
(![]() )的图象G上,
)的图象G上,
∴ m= 4;
(2)①当n=5时,直线![]() 经过点B(1,5),
经过点B(1,5),
∴ ![]() ,解得
,解得![]() .
.
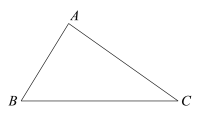
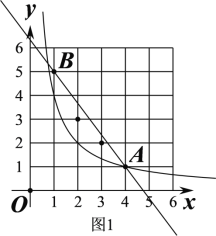
此时区域![]() 内有2个整点(2,3)、(3,2),如图1;
内有2个整点(2,3)、(3,2),如图1;
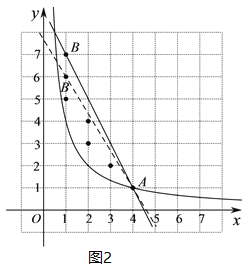
②如图2,∵直线![]() 过定点A(4,1),n为整数,
过定点A(4,1),n为整数,
∴当n=6时,直线![]() 经过点B(1,6),解得
经过点B(1,6),解得![]() ,此时区域
,此时区域![]() 内有4个整点;
内有4个整点;
当n=7时,直线![]() 经过点B(1,7),解得
经过点B(1,7),解得![]() ,区域
,区域![]() 内有5个整点;
内有5个整点;
∴ ![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
相关题目