题目内容
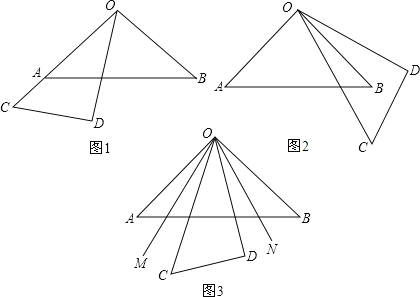
【题目】已知将一副三角板(直角三角板OAB和直角三角板OCD,∠AOB=90°,∠COD=30°)如图1摆放,点O、A、C在一条直线上.将直角三角板OCD绕点O逆时针方向转动,变化摆放如图位置
(1)如图1,当点O、A、C在同一条直线上时,则∠BOD的度数是多少?
(2)如图2,若要OB恰好平分∠COD,则∠AOC的度数是多少?
(3)如图3,当三角板OCD摆放在∠AOB内部时,作射线OM平分∠AOC,射线ON平分∠BOD,如果三角板OCD在∠AOB内绕点O任意转动,∠MON的度数是否发生变化?如果不变,求其值;如果变化,说明理由.
【答案】(1)60°;(2)75°;(3)60°.
【解析】
(1)根据∠BOD=∠AOB∠COD即可求解;
(2)∠AOC=∠AOB∠COB=90°15°=75°,故答案是60°、75°;
(3)由图可得角之间的关系:∠MON=![]() (∠AOB∠COD)+∠COD.
(∠AOB∠COD)+∠COD.
解:(1)∠BOD=90°﹣∠COD=90°﹣30°=60°;
(2)∠AOC=90°﹣![]() ∠COD=90°﹣
∠COD=90°﹣![]() ×30°=75°;
×30°=75°;
(3)不变,总是60°;
∵∠MOC+∠DON=![]() (∠AOB﹣∠COD)
(∠AOB﹣∠COD)
=![]() ×(900﹣300)=30°,
×(900﹣300)=30°,
∴∠MON=∠MOC+∠DON+∠COD=30°+30°=60°.

【题目】某工厂为了解甲、乙两个部门员工的生产技能情况,从甲、乙两个部门各随机抽取20名员工,进行生产技能测试,测试成绩(百分制)如下:
甲7886 748175768770759075798170748086698377
乙9373 888172819483778380817081737882807040
(说明:成绩80分及以上为优秀,70-79分为良好,60-69分为合格,60分以下为不合格)
(1)请填完整表格:
部门 | 平均数 | 中位数 | 众数 |
甲 | 78.3 | 75 | |
乙 | 78 | 80.5 |
(2)从样本数据可以推断出 部门员工的生产技能水平较高,请说明理由.(至少从两个不同的角度说明推断的合理性).