题目内容
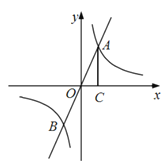
【题目】如图,正比例函数![]() 与反比例函数
与反比例函数![]() 的图像交于A,B两点,过点A作AC⊥x轴,垂足为C,△ACO的面积为4。
的图像交于A,B两点,过点A作AC⊥x轴,垂足为C,△ACO的面积为4。
(1)求反比例函数的表达式;
(2)点B的坐标为 ;
(3)当![]() 时,直接写出x的取值范围。
时,直接写出x的取值范围。
【答案】解: ![]() ;
;
(2)B(-2,-4);
(3)-2<x<0或x>2.
【解析】
(1)根据反比例函数图象的性质,反比例函数上任意一点向x轴(或y轴)作垂线,这一点、所交点与原点之间所围成的直角三角形的面积等于![]() ,图象经过一、三象限k>0;
,图象经过一、三象限k>0;
(2)联立正比例函数与反比例函数,解出的x,y分别为交点的横、纵坐标,这里需注意解得的解集有两个,说明交点有两个,需要考虑点所在位于哪一个象限;
(3)观察图像可以解决问题,谁的图像在上面,谁对应的函数值大,这里需过两个交点作x轴垂线,两条垂线与y轴将图象分成四部分,分别讨论.
解:(1)∵△ACO的面积为4,C⊥x轴
∴![]() ,
,
即![]() ,
,
∵点A是函数![]() 的点
的点
∴![]() ,
,
∵反比例函数的图像在第一、三象限,
∴k>0
∴k=8,反比例函数表达式为![]() ;
;
(2)联立 ,可解得
,可解得![]() 或
或![]() ,
,
∵B点在第三象限,
∴点B坐标为(-2,-4).
(3)根据(2)易得A点坐标为(2,4),
所以当-2<x<0或x>2时,![]()

练习册系列答案
相关题目
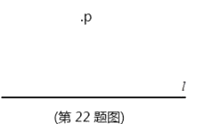
【题目】在数学课上,同学们已经探究过“经过已知直线外一点作这条直线的垂线”的尺规作图过程:
已知:直线
求作:直线 做法:如图:(1)在直线 (2)分别以点 (3)作直线 |
参考以上材料作图的方法,解决以下问题:
(1)以上材料作图的依据是 .
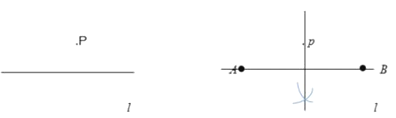
(3)已知:直线![]() 和
和![]() 外一点
外一点![]() ,
,
求作:![]() ,使它与直线
,使它与直线![]() 相切。(尺规作图,不写做法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑)
相切。(尺规作图,不写做法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑)