题目内容
【题目】等腰△ABC中,∠BAC=120°,AB=AC=6,点D为边BC上一动点.将△ABD沿着AD对折到△AB′D.若△BB′D为直角三角形,则BD=___________

【答案】![]() 或
或![]()
【解析】
首先作AE⊥BC,垂足为E,
解:如图所示,作AE⊥BC,垂足为E,根据等腰三角形的对称性,分两种情况:点D在点E左侧和右侧. ①当点D在点E左侧时,根据等腰三角形的性质,可得AE=3,BE=![]() ,∠ABD=30°,∠BAE=60°,又因为将△ABD沿着AD对折到△AB′D,可得AB=A B′,∠ABD=∠AB′D,∠BAD=∠B′AD=15°,又△BB′D为直角三角形,得出B′D∥AE,∠AB′D=∠B′AE=30°,进而得出∠DAE=45°,即DE=AE=3,即可求出BD=
,∠ABD=30°,∠BAE=60°,又因为将△ABD沿着AD对折到△AB′D,可得AB=A B′,∠ABD=∠AB′D,∠BAD=∠B′AD=15°,又△BB′D为直角三角形,得出B′D∥AE,∠AB′D=∠B′AE=30°,进而得出∠DAE=45°,即DE=AE=3,即可求出BD=![]() ;②当点D在点E右侧时,同理可得BD=
;②当点D在点E右侧时,同理可得BD=![]() ;综合起来,即得出BD.
;综合起来,即得出BD.
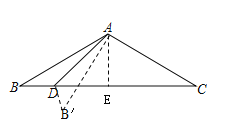
根据等腰三角形的对称性,分两种情况:点D在点E左侧和右侧.
① 当点D在点E左侧时,
∵等腰△ABC中,∠BAC=120°,AB=AC=6,
∴AE=3,BE=![]() ,∠ABD=30°,∠BAE=60°,
,∠ABD=30°,∠BAE=60°,
又∵将△ABD沿着AD对折到△AB′D,
∴AB=A B′,∠ABD=∠AB′D,∠BAD=∠B′AD=15°,
又△BB′D为直角三角形,即B′D⊥BC,
∴B′D∥AE,
∴∠AB′D=∠B′AE=30°
∴∠DAE=45°,即DE=AE=3,
∴BD=![]()
② 当点D在点E右侧时,
同理可得BD=![]() .
.
综上所述,BD=![]() 或
或![]() .
.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目