题目内容
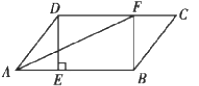
【题目】如图,在正方形ABCD中,点E、F、H分别是AB、BC、CD的中点,CE、DF交于点G,连接AG、HG。下列结论:①CE⊥DF;②AG=DG;③∠CHG=∠DAG。其中,正确的结论有( )

A. 0个B. 1个C. 2个D. 3个
【答案】C
【解析】
连接AH,由四边形ABCD是正方形与点E、F、H分别是AB、BC、CD的中点,容易证得△BCE≌△CDF与△ADH≌△DCF,根据全等三角形的性质,容易证得CE⊥DF与AH⊥DF,故①正确;根据垂直平分线的性质,即可证得AG=AD,继而AG=DC,而DG≠DC,所以AG≠DG,故②错误;由直角三角形斜边上的中线等于斜边的一半,即可证得HG=![]() DC,∠CHG=2∠GDC,根据等腰三角形的性质,即可得∠DAG=2∠DAH=2∠GDC.所以∠DAG=∠CHG,④正确,则问题得解.
DC,∠CHG=2∠GDC,根据等腰三角形的性质,即可得∠DAG=2∠DAH=2∠GDC.所以∠DAG=∠CHG,④正确,则问题得解.

∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠B=∠BCD=90°,
∵点E. F. H分别是AB、BC、CD的中点,
∴BE=FC
∴△BCE≌△CDF,
∴∠ECB=∠CDF,
∵∠BCE+∠ECD=90°,
∴∠ECD+∠CDF=90°,
∴∠CGD=90°,
∴CE⊥DF,故①正确;
连接AH,
同理可得:AH⊥DF,
∵CE⊥DF,
∴△CGD为直角三角形,
∴HG=HD=![]() CD,
CD,
∴DK=GK,
∴AH垂直平分DG,
∴AG=AD=DC,
在Rt△CGD中,DG≠DC,
∴AG≠DG,故②错误;
∵AG=AD, AH垂直平分DG
∴∠DAG=2∠DAH,
根据①,同理可证△ADH≌△DCF
∴∠DAH=∠CDF,
∴∠DAG=2∠CDF,
∵GH=DH,
∴∠HDG=∠HGD,
∴∠GHC=∠HDG+∠HGD=2∠CDF,
∴∠GHC=∠DAG,故③正确,
所以①和③正确选择C.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案