题目内容
【题目】如图，点A的坐标为（﹣
，0），点B的坐标为（0，3）．
（1）求过A，B两点直线的函数表达式；
（2）过B点作直线BP与x轴交于点P，且使OP=2OA，求△ABP的面积．
【答案】（1）过A，B两点的直线解析式为y=2x+3；
（2）△ABP的面积为
或
．
【解析】
（1）设直线l的解析式为y=ax+b，把A、B的坐标代入求出即可；
（2）分为两种情况：①当P在x轴的负半轴上时，②当P在x轴的正半轴上时，求出AP，再根据三角形面积公式求出即可．
解：（1）设过A，B两点的直线解析式为y=ax+b（a≠0），
则根据题意，得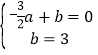
，
解得:
，
则过A，B两点的直线解析式为y=2x+3；
（2）设P点坐标为（x，0），依题意得x=±3，
∴P点坐标分别为P1（3，0），P2（﹣3，0），
=，
=，
故△ABP的面积为或．
练习册系列答案
相关题目
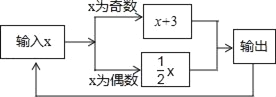
【题目】有一数值转换器，原理如图所示，
（1）如果开始输入x的值是1，可发现第一次输出的是4，第二次输出的是 ，第三次输出的是 ，第4次输出的是 …，请根据你的发现填写如表：
输出次数 | 1 | 2 | 3 | 4 | 5 | … | 3n | 3n+1 | 3n+2 |
输出的数 | 4 |
| 1 |
|
| … |
|
|
|
（2）如果开始输入的数是11，可发现第一次输出的是14，第二次输出的是7，…“，请你探索第2017次和2018次输出的结果．
