Question

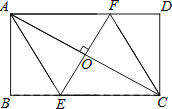
【题目】如图（1），在矩形ABCD中，BC=8，点P是BC边上一点，且BP=3，点E是线段CD上的一个动点，把△PCE沿PE折叠，点C的对应点为点F，当点E与点D重合时，点F恰好落在AB上．

（1）求CD的长；

（2）若点F刚好落在线段AD的垂直平分线上时，求线段CE的长；

（3）请直接写出AF的最小值.

Answer 1

【答案】（1）10；（2）y=(或)；（3）.

【解析】

如图1中，设CD=x，由折叠可知：,在RT△PBF中，求得AF=x-4，在RT△AFD中，根据AD2+AF2=DF2，构建方程即可解决问题．

如下图2所示，MN是线段AD的中垂线，作FG⊥CD于H．设CE=y，根据RT△PNF，求得FN=, CG=FN,GE=-y，在RT△GEF中，根据FG2+GE2=EF2，构建方程即可解决问题．

要使AF最小，当且仅当点A、F、P在同一直线上.

（1）当点E与点D重合时，如图

设CD=x，

由折叠可知：DF=DC=x, PC=PF=5,

在RT△PBF中，

BF=

则 AF=x-4，

在RT△AFD中，∠A=90°

由AD2+AF2=DF2

得

解得：x=10,即CD=10.

（2）当点F落在AD得中垂线MN上时，

作FG⊥DC于点G，则FG=4，

在RT△PNF中，

FN=

设CE=y，∵CG=FN=，

∴GE=-y，

在RT△GEF中，由FG2+GE2=EF2

得：42+（-y）2=y2

解之得：y=(或)

要使AF最小，当且仅当点A、F、P在同一直线上