��Ŀ����
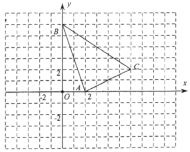
����Ŀ�����壺��ƽ��ֱ������ϵ�У�����P�Ƶ�T��t��0����t��0����ת180��õ���Q����Ƶ�QΪ��P�ġ���չ�㡱��
��1����t��3ʱ���㣨0��0���ġ���չ�㡱����Ϊ�� �����㣨��1����1���ġ���չ�㡱����Ϊ�� ����
��2����t��2����㣨2��3���ġ���չ�㡱�ĺ�����Ϊ�� �����ú�t�Ĵ���ʽ��ʾ ����
��3������P��ֱ��y��2x+6�ϣ��䡰��չ�㡱Q��ֱ��y��2x��8�ϣ����T�����꣮
��4����P��2��2����������y����x2+k�ϣ���M�������������ϣ���QΪ��P�ġ���չ�㡱������PMQ���Ե�MΪֱ�Ƕ���ĵ���ֱ�������Σ���t��ֵ��
���𰸡���1����6��0������7��1������2��2t��2����3��T��![]() ��0������4��t��ֵΪ
��0������4��t��ֵΪ![]() ��5��
��5��
��������
��1���������ν�ϵ�˼������ĶԳƵ�������⣻
��2���������ν�ϵ�˼������ĶԳƵ�������⣻
��3����![]() ��
��![]() ��
��![]() ���
���![]() �����
�����![]() �Գƣ������е����깫ʽ�õ�
�Գƣ������е����깫ʽ�õ�![]() ��
��![]() ��Ȼ�����
��Ȼ�����![]() �õ�
�õ�![]() �����ꣻ
�����ꣻ
��4���Ȱ�![]() ����
����![]() �����
�����![]() �õ������߽���ʽΪ
�õ������߽���ʽΪ![]() �����õ�
�����õ�![]() Ϊ��
Ϊ��![]() ������չ�����õ���
������չ�����õ���![]() Ϊ
Ϊ![]() ���е㣬�ٸ��ݵ���ֱ�������ε����ʵõ�
���е㣬�ٸ��ݵ���ֱ�������ε����ʵõ�![]() Ϊ����ֱ�������Σ����ۣ���
Ϊ����ֱ�������Σ����ۣ���![]() ʱ����
ʱ����![]() ����
����![]() ��˳ʱ����ת
��˳ʱ����ת![]() �õ���
�õ���![]() ��������ת��������
��������ת��������![]() ��Ȼ��
��Ȼ��![]() ����������
����������![]() ��
��![]() ���ٽⷽ�̼��ɣ���
���ٽⷽ�̼��ɣ���![]() ʱ������ͬ���������Ӧ
ʱ������ͬ���������Ӧ![]() ��ֵ��
��ֵ��
��1���ѣ�0��0���Ƶ㣨3��0����ת180���õ��������Ϊ��6��0����
�ѣ���1����1���Ƶ㣨3��0����ת180���õ��������Ϊ��7��1����
��2���ѣ�2��3���Ƶ㣨t��0����ת180���õ��������Ϊ��2t��2����3����
�ʴ�Ϊ��6��1������7��1����2t��2��
��3����P��m��2m+6����Q��n��2n��8����
��P���Q�����T��t��0���Գƣ�
��![]() ��0��
��0��![]() ��t��
��t��
��m+n��1��t��![]() ��
��
��T��![]() ��0����
��0����
��4���ѣ�2��2������y����x2+k�é�4+k��2��
���k��6��
�������߽���ʽΪy����x2+6��
�ߵ�QΪ��P������չ������
���TΪPQ���е㣬
�ߡ�PMQ���Ե�MΪֱ�Ƕ���ĵ���ֱ�������Σ�
��MT��ֱƽ��PQ��
���PTMΪ����ֱ�������Σ�
��0��t��2ʱ��
��P����T��˳ʱ����ת90���õ���M��
��M��t+2��t��2����
��M��t+2��t��2������y����x2+6���t+2��2+6��t��2��
���t1��![]() ��t2��
��t2��![]() ����ȥ����
����ȥ����
��t��2ʱ��
��P����T����ʱ����ת90���õ���M��
��M��t��2��2��t����
��M��t��2��2��t������y����x2+6���t��2��2+6��2��t��
���t1��5��t2��0����ȥ����
����������t��ֵΪ![]() ��5��
��5��

 һŵ��ҵ�����ҵ���ּ�����������������ϵ�д�
һŵ��ҵ�����ҵ���ּ�����������������ϵ�д�����Ŀ������ɽԺʿ̸����������״��������ʱ˵����������Ҫ���ӷ�������Ҳ���ؿֻţ�������ȥ��Ա�ܼ��ij��������Ŵ����֣�������ע��ͨ�磬��ϴ�֣����˶����ٰ�ҹ������ij����Ϊ�˼�ǿ�������������״����������֪ʶ���˽⣬ͨ����Ⱥ��������״�������ķ���֪ʶ�������������������߲�������2020������״��������ȫ��ͳһ���ԣ�ȫ���������Ծ�����������Ա����Ӽס�������С������ȡ20����Ա�Ĵ���ɼ����������ǵijɼ�����λ���֣�����ͳ�ơ��������������£�
�ռ����ݣ�
������ | 85 | 80 | 95 | 100 | 90 | 95 | 85 | 65 | 75 | 85 | 90 | 90 | 70 |
90 | 100 | 80 | 80 | 90 | 95 | 75 | |||||||
������ | 80 | 60 | 80 | 95 | 65 | 100 | 90 | 85 | 85 | 80 | 95 | 75 | 80 |
90 | 70 | 80 | 95 | 75 | 100 | 90 |
�������ݣ�
�ɼ� x���֣� | 60��x��70 | 70��x��80 | 80��x��90 | 90��x��100 |
���� | 2 | 5 | a | b |
���� | 3 | 7 | 5 | 5 |
�������ݣ�
ͳ���� | ƽ���� | ��λ�� | ���� |
���� | 85.75 | 87.5 | c |
���� | 83.5 | d | 80 |
Ӧ�����ݣ�
��1����գ�![]() �� ��
�� ��![]() �� ��
�� ��![]() �� ��
�� ��![]() �� ��
�� ��
��2������С������800�˲�����������Ƽ�С���ɼ�����90�ֵ�������
��3����������Ա����ͳ�����ݣ����ӳɼ���60��70��֮�������С���������ȡ2�˽����ٲ��ԣ��������ȡ������ǡ��һ���Ǽ�С����һ������С���ĸ��ʣ�