题目内容
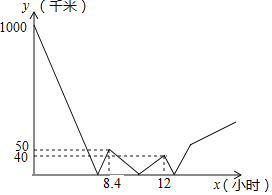
【题目】在同一直线上有A、B两地,甲车从A地送货到B地,同时乙车从B地前往A地,两车皆匀速行驶.途中某一时刻,甲车发现有货物落在A、B之间的某处C地,于是立刻掉头并以自己原来速度的两倍匀速返回,取到货物后,再以最初的速度继续匀速向B地行驶.两车之间的距离y(千米)与甲车行驶的时间x(小时)之间的函数关系如图所示(途中掉头、取货物耽误时间忽略不计),当乙车到达A地时,甲车到A地的距离为_____千米.
【答案】![]() .
.
【解析】
根据图像,AB两地相距1000千米,第一次与x轴相交时,说明甲乙两车相遇并继续向前开,x=8.4时,两车相距50千米,由此可以甲车和乙车速度列等量关系.因为图像由向上变为向下,说明甲车此时开始掉头以两倍速度追击乙车,在x=12时追上并且超过乙车40千米,可以据此再列关于甲车和乙车速度得等量关系,联立刚才的方程,并解出甲车和乙车的速度.根据前8.4小时的路程减去3.6小时返回的路程,算出甲车此时距离A地的距离,再算出乙车到达A地时的时间,减去12小时即为甲车接下来走的时间,可算出接下来甲车走的距离,加上之前的距离可以得此时距离A地的距离.
由图象可知,AB两地相距1000千米,
相遇后,8.4小时两车相距50千米,说明两车各行驶8.4小时的路程和比AB两地的路程1000千米要多50千米,即:8.4×(v甲+v乙)=1000+50,
所以,v甲+v乙=125千米/小时,
返回后,甲以2倍速度行驶3.6小时的路程与乙行驶3.6小时的路程相差40+50=90千米,即:2v甲×3.6=v乙×3.6+90,也就是,2v甲﹣v乙=25,
故求出,v甲=50千米/小时,v乙=75千米/小时,
于是AC之间的路程为50×8.4﹣100×3.6=60千米,
乙车行全程的时间为1000÷75=![]() 小时,
小时,
当乙车到达A地时,甲车从C地又行驶(![]() ﹣12)=
﹣12)=![]() 小时,
小时,
因此,甲车距A地距离为:60+50×![]() =
=![]() 千米.
千米.
故答案为:![]() .
.

 期末1卷素质教育评估卷系列答案
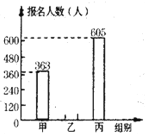
期末1卷素质教育评估卷系列答案【题目】中华文明,源远流长;中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | 40 | n |
80≤x<90 | m | 0.35 |
90≤x≤100 | 50 | 0.25 |
请根据所给信息,解答下列问题:
(1)m= ,n= ;
(2)请补全频数分布直方图;
(3)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有多少人?