题目内容
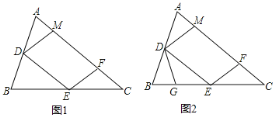
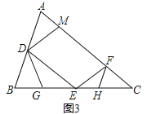
【题目】已知如图1,四边形![]() 是正方形,
是正方形,![]() 分别在边
分别在边![]() 、
、![]() 上,且
上,且![]() ,我们把这种模型称为“半角模型”,在解决“半角模型”问题时,旋转是一种常用的方法.
,我们把这种模型称为“半角模型”,在解决“半角模型”问题时,旋转是一种常用的方法.
(1)在图l中,连接![]() ,为了证明结论“
,为了证明结论“![]() ”,小亮将
”,小亮将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 后解答了这个问题,请按小亮的思路写出证明过程;
后解答了这个问题,请按小亮的思路写出证明过程;
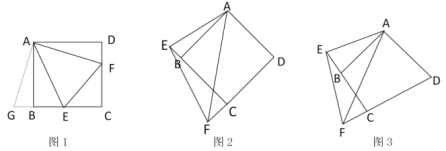
(2)如图2,当![]() 绕点
绕点![]() 旋转到图2位置时,试探究
旋转到图2位置时,试探究![]() 与
与![]() 、
、![]() 之间有怎样的数量关系?
之间有怎样的数量关系?
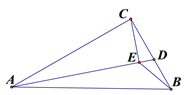
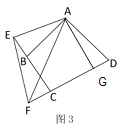
(3)如图3,如果四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)![]() ,见解析;(3)
,见解析;(3)![]() 的长为5.
的长为5.
【解析】
(1)利用旋转的性质和正方形的性质,证明![]() 即可求证;
即可求证;
(2)在![]() 上取一点
上取一点![]() ,使
,使![]() ,先证明
,先证明![]() ,再证明
,再证明![]() ,即可得出答案;
,即可得出答案;
(3)在![]() 上取一点
上取一点![]() ,使
,使![]() ,先证明
,先证明![]() ,再证明
,再证明![]() ,得到EF=FG,设
,得到EF=FG,设![]() ,用含x的代数式表达GC和EF,根据勾股定理列出方程,解出x的值即可.
,用含x的代数式表达GC和EF,根据勾股定理列出方程,解出x的值即可.
(1)证明:∵![]() ,
,
∴![]() ,
,![]() ,
,
∵∠EAF=45°,
∴∠DAF+∠BAE=45°,即∠GAB+∠BAE=45°,
∴∠GAE=∠EAF,
∴在△GAE和△FAE中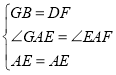 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)解:在![]() 上取一点
上取一点![]() ,使
,使![]() ,
,
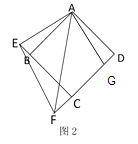 ,
,
∵四边形ABCD是正方形,
∴AD=AB,∠ADG=∠ABE=90°,
又∵DG=BE,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵∠EAF=∠BAE+∠BAF=45°,
∴∠GAD+∠BAF=45°,
∴∠GAF=45°,即∠EAF=∠GAF,
∴![]() ,
,
∴![]() ,
,
即![]() ;
;
(3)解:在![]() 上取一点
上取一点![]() ,使
,使![]() ,
,
∵![]() ,
,
∴∠D+∠ABC=180°,
∵∠ABE+∠ABC=180°,
∴∠D=∠ABE,
又∵AB=AD,DG=BE,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵∠EAF=∠BAE+∠BAF=45°,
∴∠GAD+∠BAF=45°,
∴∠GAF=45°,即∠EAF=∠GAF,
∴![]() ,
,
∴EF=FG
设![]()
∴![]() ,
,
∴![]()
在![]() 中,
中,![]()
∴![]() ,
,
解得:![]() ,
,
答:![]() 的长为5.
的长为5.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案【题目】我市某工艺厂为配合北京奥运,设计了一款成本为20元∕件的工艺品投放市场进行试销.经过调查,得到如下数据:
销售单价x(元/件) | … | 30 | 40 | 50 | 60 | … |
每天销售量y(件) | … | 500 | 400 | 300 | 200 | … |
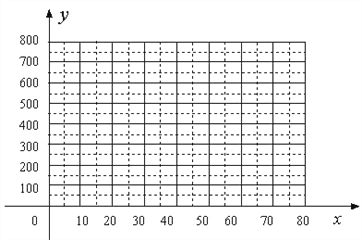
(1)把上表中x、y的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想y与x的函数关系,并求出函数关系式;
(2)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?(利润=销售总价﹣成本总价)
(3)当地物价部门规定,该工艺品销售单价最高不能超过45元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?
【题目】中华文明,源远流长;中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | 40 | n |
80≤x<90 | m | 0.35 |
90≤x≤100 | 50 | 0.25 |
请根据所给信息,解答下列问题:
(1)m= ,n= ;
(2)请补全频数分布直方图;
(3)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有多少人?