题目内容
【题目】某市中招体育测试改革,其中篮球和足球作为选考项目,某商店抓住这一商机决定购进一批篮球和足球共200个,这两种球的进价和售价如下表所示:
篮球 | 足球 | |
进价(元/个) | 180 | 150 |
售价(元/个) | 250 | 200 |
(1)若商店计划销售完这批球后能获利11600元,问篮球和足球应分别购进多少个?
(2)设购进篮球![]() 个,获利为
个,获利为![]() 元,求
元,求![]() 与
与![]() 之间的函数关系;
之间的函数关系;
(3)若商店计划投入资金不多于31560元且销售完这批球后商店获利不少于11000元,请问有哪几种购球方案,并写出获利最大的购球方案.
【答案】(1)购进篮球80个,购进足球120个;(2)![]() ;(3)3种购球方案见解析;获利最大的购球方案为购进篮球52个,购进足球148个.
;(3)3种购球方案见解析;获利最大的购球方案为购进篮球52个,购进足球148个.
【解析】
(1)购进篮球![]() 个,则购进足球
个,则购进足球![]() ,根据题中等量关系列出方程,求得m值;
,根据题中等量关系列出方程,求得m值;
(2)根据总获利等于篮球的获利加上足球的获利列出函数关系式即可;
(3)根据投入资金不多于31560元且销售完这批球后商店获利不少于11000元,列出不等式组,求得x的取值范围,又因为x为整数,可确定x的取值,然后利用一次函数的性质可得获利最大的购球方案.
(1)设购进篮球![]() 个,则购进足球
个,则购进足球![]() 个,
个,
由题意,得:![]() ,
,
解得:![]() ,
,
![]() ,
,
即购进篮球80个,购进足球120个;
(2)设购进篮球x个,则购进足球![]() 个,
个,
由题意,可得![]()
![]() ,
,
即![]() ;
;
(3)由题意,得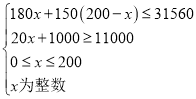 ,
,
解得:![]() ,且
,且![]() 为整数,
为整数,
![]() 共有3种方案,如下表
共有3种方案,如下表
篮球 | 足球 | |
方案一 | 50 | 150 |
方案二 | 51 | 149 |
方案三 | 52 | 148 |
![]() 中
中![]() ,
,
![]() 随
随![]() 的增大而增大
的增大而增大
![]() 当
当![]() 时,
时,![]() 取得最大值.
取得最大值.
即获利最大的购球方案为:购进篮球52个,购进足球148个.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目