Question

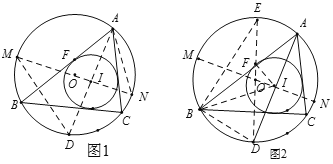
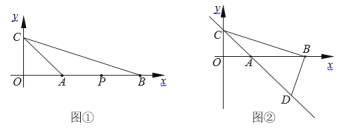
【题目】定义：点P在△ABC的边上，且与△ABC的顶点不重合．若满足△PAB、△PBC、△PAC至少有一个三角形与△ABC相似（但不全等），则称点P为△ABC的自相似点．如图①，已知点A、B、C的坐标分别为（1，0）、（3，0）、（0，1）．

（1）若点P的坐标为（2，0），求证点P是△ABC的自相似点；

（2）求除点（2，0）外△ABC所有自相似点的坐标；

（3）如图②，过点B作DB⊥BC交直线AC于点D，在直线AC上是否存在点G，使△GBD与△GBC有公共的自相似点？若存在，请举例说明；若不存在，请说明理由．

Answer 1

【答案】（1）见解析；（2）△CPA∽△CAB，此时P（，）；△BPA∽△BAC，此时P(，)；（3）S（3，-2）是△GBD与△GBC公共的自相似点，见解析

【解析】

（1）利用：两边对应成比例且夹角相等,证明△APC∽△CAB即可；

（2）分类讨论：△CPA∽△CAB和△BPA∽△BAC，分别求得P点的坐标；

（3）先求得点D的坐标，说明点G（5，）、S（3，-2）在直线AC：上，证得△ABC△SGB，再证得△GBS∽△GCB，说明点S是△GBC的自相似点；又证得△DBG△DSB，说明点S是△GBD的自相似点．从而说明S（3，-2）是△GBD与△GBC公共的自相似点.

（1）如图，

∵A（1，0），B（3，0），C（0，1），P（2，0），

∴AP=2－1＝1，

AC=，

AB=3-1=2，

∴，，

∴=，

∵∠PAC=∠CAB，

∴△APC∽△CAB，

故点P是△ABC的自相似点；

（2）点P只能在BC上，

①△CPA∽△CAB，如图，

由(1)得：AC，AB，

又，

∵△CPA∽△CAB，

∴，

∴，

∴，

过点P作PD∥y轴交轴于D，

∴，，

∴，，

∴，，

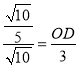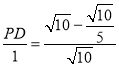P点的坐标为(，)

②△BPA∽△BAC，如图，

由前面获得的数据：AB，，

∵△BPA∽△BAC，

∴，

∴，

∴，

过点P作PE∥y轴交轴于E，

∴，

∴，

∴，，

∴，

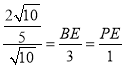P点的坐标为(，)；

（3）存在．当点G的坐标为（5，）时，△GBD与△GBC公共的自相似点为S（3，）．理由如下：

如图：

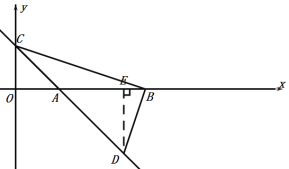
设直线AC的解析式为：，
∴，

解得：，

∴直线AC的解析式为：，

过点D作DE⊥x轴于点E，
∵∠CBO+∠DBE=90，∠EDB+∠DBE=90，

∴∠CBO=∠EDB，

∴，

∴，

设BE=a，则DE=3a，

∴OE=3-a，

∴点D的坐标为(3-a，-3a) ，

∵点D在直线AC上，

∴，

解得：，

∴点D的坐标为(，) ；

如下图：当点G的坐标为（5，）时，△GBD与△GBC公共的自相似点为S（3，）．

直线AC的解析式为：，
∵，，

∴点G、点S在直线AC上，

过点G作GH⊥x轴于点H，

∵，

∴，

由S（3，）、B（3，0）知BS⊥x轴，

∴△AED、△ABS、△AHG为等腰直角三角形，

∵D (，)，S，G( ，

∴，，B，

，

，，

，，，

，

在△ABC和△SGB中

∵，，

∴，

∵

∴

∴△ABC△SGB

∴∠SBG=∠BCA，

又∠SGB=∠BGC，

∴△GBS∽△GCB，

∴点S是△GBC的自相似点；

在△DBG和△DSB中，

∵，，

∴，且，

∴△DBG△DSB；

∴点S是△GBD的自相似点．

∴S（3，）是△GBD与△GBC公共的自相似点．