题目内容
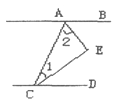
【题目】如图,已知AB∥CD,CE、AE分别平分![]() 、
、![]() ,则
,则![]() = ( )
= ( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】
由AB∥CD,根据两直线平行,同旁内角互补,可得∠BAC+∠ACD=180°,又由CE、AE分别平分∠ACD、∠CAB,可得![]() ,
,![]() ,则可求得∠1+∠2的度数.
,则可求得∠1+∠2的度数.
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∵CE、AE分别平分∠ACD、∠CAB,
∴![]() ,
,![]() ,
,
∴![]() .
.
故选B.
【考点精析】通过灵活运用平行线的性质和三角形的内角和外角,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角即可以解答此题.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目