题目内容
如图,⊙O1与⊙O2相交,大圆⊙O1的弦AB⊥O1O2,垂足是F,且交⊙O2于点C,D,过B作⊙O2的切线,E为切点,已知BE=DE,BD=m,BE=n,AC,CE的长是关于x的方程x2+px+q=0的两个根.(1)求证:AC=BD;
(2)用含m,n的代数式分别表示p和q;
(3)如果关于x的方程qx2-(m2+mp)x+1=0有两个相等的实数根,且∠DEB=30°,求⊙O2的半径.
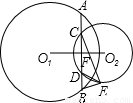
【答案】分析:(1)由垂径定理可知FA=FB,FC=FD,所以AC=BD;
(2)由已知条件证明△CBE∽△EBD可得:BC= =
= ,证明△CBE∽△EBD可得
,证明△CBE∽△EBD可得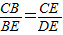 ,因为BE=DE,所以CE=CB=
,因为BE=DE,所以CE=CB= ,又AC=BD=m,所以p=-(AC+CE)=-(m+
,又AC=BD=m,所以p=-(AC+CE)=-(m+ )=-
)=- ,q=AC•CE=m•
,q=AC•CE=m•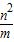 =n2;
=n2;
(3)因为方程qx2-(m2+mp)x+1=0有两个相等的实数根,所以△=[-(m2+mp)]2-4q=(-n2)2-4n2=0,连接O2D,O2E,证明△O2ED是等边三角形,即可得到O2E=DE=BE=2.
解答:解:(1)∵O1F⊥AB,
∴FA=FB.
∵O2F⊥CD,
∴FC=FD,
∴AC=BD;
(2)∵BE和⊙O2切于点E,
∴BE2=BD•BC,
∴BC= =
= ,
,
又∵∠BCE=∠DEB,∠B=∠B,
∴△CBE∽△EBD,
∴ ,
,
∵BE=DE,
∴CE=CB= ,
,
又∵AC=BD=m,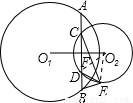
∴p=-(AC+CE)=-(m+ )=-
)=- ,q=AC•CE=m•
,q=AC•CE=m•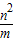 =n2;
=n2;
(3)∵方程qx2-(m2+mp)x+1=0有两个相等的实数根,
而p=- •q=n2,
•q=n2,
∴△=[-(m2+mp)]2-4q=(-n2)2-4n2=0.
由n>0,
解得n=2.
连接O2D,O2E.
又∵∠DEB=30°,∠BEO2=90°,
∴∠O2ED=60°,
∴△O2ED是等边三角形,
∴O2E=DE=BE=2,
即⊙O2的半径是2.
点评:本题考查了垂径定理、相似三角形的判定和性质、根的判别式的应用以及等边三角形的判定和性质,此题将两圆相交的条件以及和两圆相关的线段和角巧妙地结合起来,使之成为一个有机的整体,要充分利用它们之间的关系.
(2)由已知条件证明△CBE∽△EBD可得:BC=
 =
= ,证明△CBE∽△EBD可得
,证明△CBE∽△EBD可得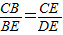 ,因为BE=DE,所以CE=CB=
,因为BE=DE,所以CE=CB= ,又AC=BD=m,所以p=-(AC+CE)=-(m+
,又AC=BD=m,所以p=-(AC+CE)=-(m+ )=-
)=- ,q=AC•CE=m•
,q=AC•CE=m•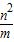 =n2;
=n2;(3)因为方程qx2-(m2+mp)x+1=0有两个相等的实数根,所以△=[-(m2+mp)]2-4q=(-n2)2-4n2=0,连接O2D,O2E,证明△O2ED是等边三角形,即可得到O2E=DE=BE=2.
解答:解:(1)∵O1F⊥AB,
∴FA=FB.
∵O2F⊥CD,
∴FC=FD,
∴AC=BD;
(2)∵BE和⊙O2切于点E,
∴BE2=BD•BC,
∴BC=
 =
= ,
,又∵∠BCE=∠DEB,∠B=∠B,
∴△CBE∽△EBD,
∴
 ,
,∵BE=DE,
∴CE=CB=
 ,
,又∵AC=BD=m,

∴p=-(AC+CE)=-(m+
 )=-
)=- ,q=AC•CE=m•
,q=AC•CE=m•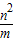 =n2;
=n2;(3)∵方程qx2-(m2+mp)x+1=0有两个相等的实数根,
而p=-
 •q=n2,
•q=n2,∴△=[-(m2+mp)]2-4q=(-n2)2-4n2=0.
由n>0,
解得n=2.
连接O2D,O2E.
又∵∠DEB=30°,∠BEO2=90°,
∴∠O2ED=60°,
∴△O2ED是等边三角形,
∴O2E=DE=BE=2,
即⊙O2的半径是2.
点评:本题考查了垂径定理、相似三角形的判定和性质、根的判别式的应用以及等边三角形的判定和性质,此题将两圆相交的条件以及和两圆相关的线段和角巧妙地结合起来,使之成为一个有机的整体,要充分利用它们之间的关系.

练习册系列答案
相关题目
 12、已知:如图,⊙O1与⊙O2外切于点P,直线AB过点P交⊙O1于A,交⊙O2于B,点C、D分别为⊙O1、⊙O2上的点,且∠ACP=65°,则∠BDP=
12、已知:如图,⊙O1与⊙O2外切于点P,直线AB过点P交⊙O1于A,交⊙O2于B,点C、D分别为⊙O1、⊙O2上的点,且∠ACP=65°,则∠BDP= 已知:如图,⊙O1与⊙O2外切于M点,AF是两圆的外公切线,A、B是切点,DF经过O1、O2,分别交⊙O1于D、⊙O2于E,AC是⊙O1的直径,BC经过M点,连接AD.
已知:如图,⊙O1与⊙O2外切于M点,AF是两圆的外公切线,A、B是切点,DF经过O1、O2,分别交⊙O1于D、⊙O2于E,AC是⊙O1的直径,BC经过M点,连接AD. 如图,⊙O1与⊙O2相交于C、D两点,⊙O1的割线PAB与DC的延长线交于点P,PN与⊙O2相切于点N,若PB=10,AB=6,则PN=
如图,⊙O1与⊙O2相交于C、D两点,⊙O1的割线PAB与DC的延长线交于点P,PN与⊙O2相切于点N,若PB=10,AB=6,则PN= 已知:如图,⊙O1与⊙O2外切于A点,直线l与⊙O1、⊙O2分别切于B,C点,若⊙O1的半径r1=2cm,⊙O2的半径r2=3cm.求BC的长.
已知:如图,⊙O1与⊙O2外切于A点,直线l与⊙O1、⊙O2分别切于B,C点,若⊙O1的半径r1=2cm,⊙O2的半径r2=3cm.求BC的长. 已知如图:⊙O1与⊙O2相交于AB两点,过点A、B的直线分别与⊙O1交于C、E,与⊙O2交于D、F,连接CE、DF.
已知如图:⊙O1与⊙O2相交于AB两点,过点A、B的直线分别与⊙O1交于C、E,与⊙O2交于D、F,连接CE、DF.