题目内容
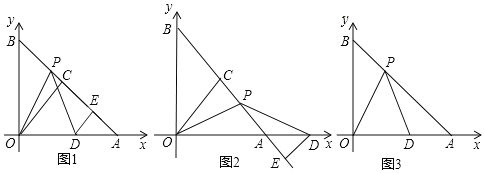
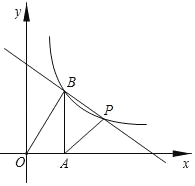
【题目】如图,在平面直角坐标系中,函数y=![]() 的图象经过点P(4,3)和点B(m,n)(其中0<m<4),作BA⊥x轴于点A,连接PA,PB,OB,已知S△AOB=S△PAB.
的图象经过点P(4,3)和点B(m,n)(其中0<m<4),作BA⊥x轴于点A,连接PA,PB,OB,已知S△AOB=S△PAB.
(1)求k的值和点B的坐标.
(2)求直线BP的解析式.
(3)直接写出在第一象限内,使反比例函数大于一次函数的x的取值范围是 .
【答案】(1)k=12;B(2,6);(2)y=﹣![]() x+9;(3)0<x<2或x>4.
x+9;(3)0<x<2或x>4.
【解析】
(1)把P(4,3)代入y=![]() ,即可求出k的值;由S△AOB=S△PAB可求出点B的横坐标,代入反比例函数解析式可求出点B的坐标;
,即可求出k的值;由S△AOB=S△PAB可求出点B的横坐标,代入反比例函数解析式可求出点B的坐标;
(2)设直线BP的解析式为y=ax+b,将B(2,6),P(4,3)代入,利用待定系数法即可求出直线BP的解析式;
(3)根据图像直接写出结论即可.
(1)将P(4,3)代入函数y=![]() ,得:k=4×3=12,
,得:k=4×3=12,
∴反比例函数为y=![]() ,
,
∵△AOB和△PAB都可以看作以AB为底,它们的面积相等,
∴它们的底AB边上的高也相等,即点O和点P到直线AB的距离相等,
∴xP=2xB,
∵P(4,3),即xP=4,
∴xB=2,
代入y=![]() ,得:y=6,
,得:y=6,
∴B(2,6);
(2)设直线BP的解析式为y=ax+b,
分别代入B(2,6)、P(4,3),
得:![]() ,
,
解得![]() ,
,
∴直线BP的解析式为y=﹣![]() x+9;
x+9;
(3)在第一象限内,反比例函数大于一次函数的x的取值范围是0<x<2或x>4,
故答案为:0<x<2或x>4.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目