Question

如图：已知E、F分别是正方形的边AB、AD中点，DE，CF相交于P，DE的延长线交CB的延长线于G，若正方形的边长为6cm，求PB的长．

Answer 1

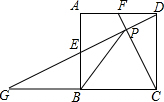
∵四边形ABCD是正方形，
∴AB=AD=CD，∠A=∠ADC=90°，
∵E、F分别是边AB、AD的中点，
∴AE=BE=DF，
∵在△ADE和△DCF中，

AE=DE ∠A=∠ADC AD=CD

，
∴△ADE≌△DCF（SAS），
∴∠ADE=∠DCF，
∵∠ADE+∠CDE=∠ADC=90°，
∴∠DCF+∠CDE=90°，
∴∠CPD=180°-90°=90°，
∴∠CPG=90°，
∵G在CB的延长线上，
∴∠EBG=180°-∠ABC=180°-90°=90°，
∴∠A=∠EBG，
∵在△ADE和△BGE中，

∠A=∠EBG AE=BE ∠AED=∠BEG

，
∴△ADE≌△BGE（ASA），
∴AD=BG，
∴PB是△PCG的中线，
∵正方形的边长为6cm，
∴CG=6+6=12cm，
∴PB=

1

2

CG=

1

2

×12=6cm．