题目内容
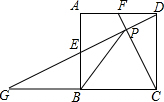
如图,在四边形ABCD中,点E是线段AD上的任意一点(E与A,D不重合),G,F,H分别是BE,BC,CE的中点.
(1)证明:四边形EGFH是平行四边形;
(2)在(1)的条件下,若EF⊥BC,且EF=
BC,证明:平行四边形EGFH是正方形.

(1)证明:四边形EGFH是平行四边形;
(2)在(1)的条件下,若EF⊥BC,且EF=
| 1 |
| 2 |

证明:(1)∵G,F分别是BE,BC的中点,
∴GF∥EC且GF=
EC.
又∵H是EC的中点,EH=
EC,
∴GF∥EH且GF=EH.
∴四边形EGFH是平行四边形.
(2)连接GH,EF.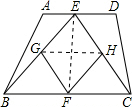
∵G,H分别是BE,EC的中点,
∴GH∥BC且GH=
BC.
又∵EF⊥BC且EF=
BC,
又∵EF⊥BC,GH是三角形EBC的中位线,
∴GH∥BC,
∴EF⊥GH,
又∵EF=GH.
∴平行四边形EGFH是正方形.
∴GF∥EC且GF=
| 1 |
| 2 |
又∵H是EC的中点,EH=
| 1 |
| 2 |
∴GF∥EH且GF=EH.
∴四边形EGFH是平行四边形.
(2)连接GH,EF.

∵G,H分别是BE,EC的中点,
∴GH∥BC且GH=
| 1 |
| 2 |
又∵EF⊥BC且EF=
| 1 |
| 2 |
又∵EF⊥BC,GH是三角形EBC的中位线,
∴GH∥BC,
∴EF⊥GH,
又∵EF=GH.
∴平行四边形EGFH是正方形.

练习册系列答案
相关题目