题目内容
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是斜边上一点,且
是斜边上一点,且![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)过点![]() 的
的![]() 与边
与边![]() 相切,切点为
相切,切点为![]() 的中点
的中点![]() ,
,![]() 与直线
与直线![]() 的另一个交点为
的另一个交点为![]() .
.
(i)求![]() 的半径;
的半径;
(ⅱ)连接![]() ,试探究
,试探究![]() 与
与![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
【答案】(Ⅰ)tan∠BCD=![]() ;(Ⅱ)(i)
;(Ⅱ)(i)![]() ;(ⅱ)AF⊥CD,理由见解析.
;(ⅱ)AF⊥CD,理由见解析.
【解析】
(Ⅰ)如图1,过D作DM⊥BC,垂足M,则DM∥AC,可得△DMB∽△ACB,根据相似三角形的性质即可求出DM和CM的长,进一步即可求出结果;
(Ⅱ)(ⅰ)如图2,连接OE,OF,根据切线的性质得到OE⊥AC,作OH⊥BE,垂足为H,则四边形OHCE为矩形,于是可得OH的长,设⊙O的半径为r,则可根据垂径定理和矩形的性质用r的代数式表示出HF的长,然后在Rt△OHF中根据勾股定理即可建立关于r的方程,解方程即得结果;
(ⅱ)如图2,延长CD,交AF于点K,先由(ⅰ)的结果求出CF的长,进一步即可求出tan∠CAF的值,与(Ⅰ)题的结果对比可得∠CAF=∠BCD,进而可根据直角三角形的性质和等量代换得出∠FCK+∠AFC=90°,于是可得结论.
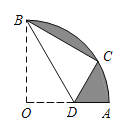
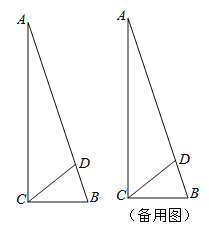
解:(Ⅰ)如图1,过D作DM⊥BC,垂足M,
∵∠ACB=90°,
∴DM∥AC.
∴△DMB∽△ACB,
∵AD=4BD,AC=3,BC=1,
∴DM=![]() AC=
AC=![]() ,CM=
,CM=![]() BC=
BC=![]() .
.
则在Rt△DMC中,tan∠DCM=![]() ,
,
即tan∠BCD=![]() ;
;

(Ⅱ)(ⅰ)如图2,连接OE,OF,
∵⊙O与AC相切于AC中点E,
∴OE⊥AC,
作OH⊥BC,垂足为H,∵∠ACB=90°,
∴四边形OHCE为矩形,
设⊙O的半径为r,则OF=OE=CH=r,
∴OH=CE=![]() AC=
AC=![]() ,HF=BH=CH﹣BC=r﹣1.
,HF=BH=CH﹣BC=r﹣1.
∴在Rt△OHF中,由勾股定理得:OF2=OH2+HF2,
∴r2=![]() +(r﹣1)2,
+(r﹣1)2,
解得r=![]() ;
;
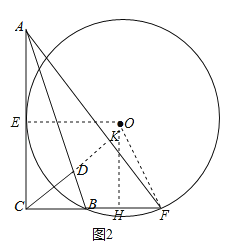
(ⅱ) AF与CD的位置关系是AF⊥CD,理由如下:
如图2,延长CD,交AF于点K,
由(ⅰ)知,CF=BC+BF=1+2(r﹣1)=![]() ,
,
∴在Rt△ACF中,∠ACB=90°,tan∠CAF=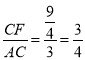 ,
,
∵tan∠BCD=![]() ,
,
∴∠CAF=∠BCD,即∠CAF=∠FCK,
∵∠CAF+∠AFC=90°,
∴∠FCK+∠AFC=90°.
即AF⊥CD.

 导学全程练创优训练系列答案
导学全程练创优训练系列答案