题目内容
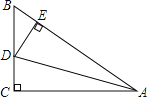
【题目】如图(a),有一张矩形纸片ABCD,其中AD=6cm,以AD为直径的半圆,正好与对边BC相切,将矩形纸片ABCD沿DE折叠,使点A落在BC上,如图(b).则半圆还露在外面的部分(阴影部分)的面积为 . 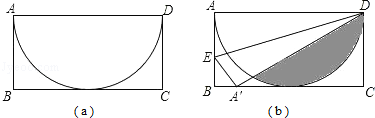
【答案】(3π﹣ ![]() )cm2
)cm2
【解析】解:作OH⊥DK于H,连接OK, ∵以AD为直径的半圆,正好与对边BC相切,
∴AD=2CD,
∴A'D=2CD,
∵∠C=90°,
∴∠DA'C=30°,
∴∠ODH=30°,
∴∠DOH=60°,
∴∠DOK=120°,
∴扇形ODK的面积为 ![]() =3πcm2 ,
=3πcm2 ,
∵∠ODH=∠OKH=30°,OD=3cm,
∴OH= ![]() cm,DH=
cm,DH= ![]() cm;
cm;
∴DK=3 ![]() cm,
cm,
∴△ODK的面积为 ![]() cm2 ,
cm2 ,
∴半圆还露在外面的部分(阴影部分)的面积是:(3π﹣ ![]() )cm2 .
)cm2 .
所以答案是:(3π﹣ ![]() )cm2 .
)cm2 .
【考点精析】掌握矩形的性质和切线的性质定理是解答本题的根本,需要知道矩形的四个角都是直角,矩形的对角线相等;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.

练习册系列答案
相关题目