题目内容
【题目】关于x的一元二次方程x2+（2m+1）x+m2﹣1=0有两个不相等的实数根，求m的取值范围；写出一个满足条件的m的值，并求此方程的根．
【答案】解：△=（2m+1）2﹣4（m2﹣1）＞0， 解得m＞﹣ 
，
当m=1时，方程为x2+3x=0，
解得x1=0，x2=﹣3
【解析】根据判别式的意义得到（2m+1）2﹣4（m2﹣1）＞0，然后解不等式得到m的范围，然后取一个满足条件的m的值代入方程，再解方程即可．
【考点精析】解答此题的关键在于理解求根公式的相关知识，掌握根的判别式△=b2-4ac，这里可以分为3种情况：1、当△>0时，一元二次方程有2个不相等的实数根2、当△=0时，一元二次方程有2个相同的实数根3、当△<0时，一元二次方程没有实数根．
练习册系列答案
冲刺100分1号卷系列答案
相关题目
【题目】A,B,C三名大学生竞选系学生会主席,他们的笔试成绩和口试成绩(单位:分)分别用了两种方式进行了统计,如下表和图①:
A | B | C | |
笔试 | 85 | 95 | 90 |
口试 | 80 | 85 |
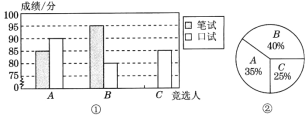
(1)请将表格和图①中的空缺部分补充完整;
(2)竞选的最后一个程序是由本系的300名学生进行投票,三位候选人的得票情况如图②(没有弃权票,每名学生只能推荐一人),请计算每人的得票数;
(3)若每票计1分,系里将笔试、口试、得票三项测试得分按4∶3∶3的比确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选.
