题目内容
【题目】已知:如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于E,且∠B+∠D=180°,
求证:AE=AD+BE.

【答案】证明见解析.
【解析】
首先在AE上截取AM=AD,连接CM,再证明△AMC≌△ADC,可得∠3=∠D,再根据∠B+∠D=180°,∠3+∠4=180°,可以证出∠4=∠B,根据等角对等边可证出CM=BC,再根据等腰三角形的性质:等腰三角形底边上的高线与底边上的中线重合可得到ME-BE,再利用等量代换可证出AE=AD+BE.
证明:在AE上截取AM=AD,连接CM,

∵AC平分∠BAD,
∴∠1=∠2,
在△AMC和△ADC中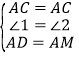 ,
,
∴△AMC≌△ADC(SAS),
∴∠3=∠D,
∵∠B+∠D=180°,∠3+∠4=180°,
∴∠4=∠B,
∴CM=CB,
∵CE⊥AB,
∴ME=EB(等腰三角形底边上的高线与底边上的中线重合),
∵AE=AM+ME,
∴AE=AD+BE.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目