Question

【题目】如图，在平面直角坐标系中，△ABC的三个顶点的坐标分别为A（-3，4），B（-4，1），C（-1，2）．
（1）在图中作出△ABC关于x轴的对称图形△A1B1C1；
（2）请直接写出点C关于y轴的对称点C'的坐标： ；
（3）△ABC的面积= ；
（4）在y轴上找一点P，使得△PAC周长最小，并求出△PAC周长的最小值．

Answer 1

【答案】（1）见解析；（2）（1，2）．（3）4 （4）．

【解析】

（1）分别作出点A，B，C关于x轴的对称点，再顺次连接即可得；
（2）由关于y轴的两点的横坐标互为相反数，纵坐标相等可得；
（3）割补法求解可得；
（4）作点C关于y轴的对称点C′，连接AC′交y轴于点P，P即为所求，此时PA+PC最小，再根据勾股定理计算可得．

解：（1）如图所示，△A1B1C1即为所求．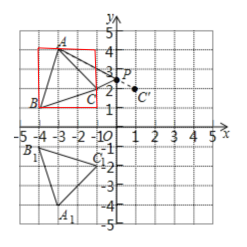


（2）点C（-1，2）关于y轴的对称点C′的坐标为（1，2），
故答案为：（1，2）．

（3）△ABC的面积=3×3-×1×3-×1×3-×2×2=4，
故答案为：4．
（4）如图，作点C关于y轴的对称点C′，连接AC′交y轴于点P，P即为所求，此时PA+PC最小，
∵PA+PC=PA+PC′=AC′=，AC=，
∴△PAC周长的最小值为．