题目内容
【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,有下列结论:①CD=ED;②AC+BE=AB;③∠BDE=∠BAC;④AD平分∠CDE;⑤S△ABD:S△ACD=AB:AC,其中正确的有( )
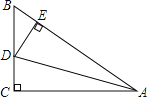
A. 5个 B. 4个 C. 3个 D. 2个
【答案】A
【解析】
:①正确,因为角平分线上的点到两边的距离相等知;
②正确,因为由HL可知△ADC≌△ADE,所以AC=AE,即AC+BE=AB;
③正确,因为∠BDE和∠BAC都与∠B互余,根据同角的补角相等,所以∠BDE=∠BAC;
④正确,因为由△ADC≌△ADE可知,∠ADC=∠ADE,所以AD平分∠CDE;
⑤正确,因为CD=ED,△ABD和△ACD的高相等,所以S△ABD:S△ACD=AB:AC.
所以正确的有五个,故选A.

练习册系列答案
相关题目