题目内容
【题目】在平面直角坐标系中,已知直线l1:y=2x+1
(1)若将直线l1平移,使之经过点(1,-5),求平移后直线的解析式;
(2)若直线l2:y=x+m与直线l1的交点在第二象限,求m的取值范围;
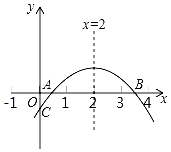
(3)如图,直线y=x+b与直线y=nx+2n(n≠0)的交点的横坐标为-5,求关于x的不等式组0<nx+2n<x+b的解集.
【答案】(1)平移后直线的解析式y=2x-7;(2)![]() <m<1;(3)-5<x<-2
<m<1;(3)-5<x<-2
【解析】
(1)利用两直线平行的问题,设平移后的直线解析式为![]() 然后把(1,-5)代入求出t即可;
然后把(1,-5)代入求出t即可;
(2)先解方程组![]() 得
得![]() 与直线
与直线![]() 的交点坐标为(m-1,2m-1),利用第二象限点的坐标特征得到
的交点坐标为(m-1,2m-1),利用第二象限点的坐标特征得到![]() ,然后解不等式组即可;
,然后解不等式组即可;
(3)写出直线![]() 在x轴上方,且直线
在x轴上方,且直线![]() 在直线
在直线![]() 的下方所对应的自变量的范围即可.
的下方所对应的自变量的范围即可.
(1)设平移后的直线解析式为y=2x+t,
把(1,-5)代入得2+t=-5,解得t=-7,
所以平移后直线的解析式y=2x-7;
(2)解方程组![]() 得
得![]() ,
,
所以y=x+m与直线l1的交点坐标为(m-1,2m-1)
因为![]()
所以![]() <m<1;
<m<1;
(3)当y=0时,nx+2n=0,解得x=-2,直线y=nx+2n与x轴的交点坐标为(-2,0),
所以不等式组0<nx+2n<x+b的解集为-5<x<-2.

【题目】A,B,C三名大学生竞选系学生会主席,他们的笔试成绩和口试成绩(单位:分)分别用了两种方式进行了统计,如下表和图①:
A | B | C | |
笔试 | 85 | 95 | 90 |
口试 | 80 | 85 |
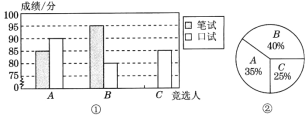
(1)请将表格和图①中的空缺部分补充完整;
(2)竞选的最后一个程序是由本系的300名学生进行投票,三位候选人的得票情况如图②(没有弃权票,每名学生只能推荐一人),请计算每人的得票数;
(3)若每票计1分,系里将笔试、口试、得票三项测试得分按4∶3∶3的比确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选.