题目内容

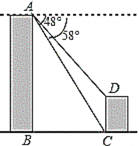
【题目】如图，甲、乙两座建筑物的水平距离为，从甲的顶部处测得乙的顶部处的俯角为48°，测得底部处的俯角为53°，求甲、乙建筑物的高度和（结果用含非特珠角的三角函数表示即可）．

【答案】，．

【解析】

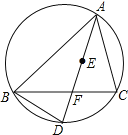
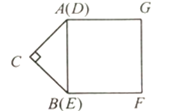
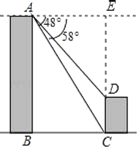
作AE⊥CD交CD的延长线于E，根据两个直角三角形的公共边构造关系，进而求解即可得出答案．

解：如图作AE⊥CD交CD的延长线于E．则四边形ABCE是矩形，

∴AE＝BC＝78，AB＝CE，．

在Rt△ACE中，EC＝AEtan58°＝78tan58°（m）

在Rt△AED中，DE＝AEtan48°＝78tan48°（m），

∴CD＝EC﹣DE＝78tan58°﹣78tan48°（m），

答：甲、乙建筑物的高度AB为78tan58°（m），DC为（78tan58°﹣78tan48°）m．

涓€棰樹竴棰樻壘绛旀瑙ｆ瀽澶參浜�
涓嬭浇浣滀笟绮剧伒鐩存帴鏌ョ湅鏁翠功绛旀瑙ｆ瀽绔嬪嵆涓嬭浇
练习册系列答案
相关题目

【题目】已知二次函数y＝ax2﹣2x＋3经过点A(﹣3，0)，P是抛物线上的一个动点．

（1）求该函数的表达式；

（2）如图所示，点P是抛物线上在第二象限内的一个动点，且点P的横坐标为t，连接AC，PA，PC．求△ACP的面积S关于t的函数关系式，并求出△ACP的面积最大时点P的坐标．

（3）连接BC，在抛物线上是否存在点P，使得∠PCA＝∠OCB？若存在，求出点P的坐标；若不存在，请说明理由．

【题目】如图，点是的内心，的延长线和的外接圆相交于点，交于．

（1）若，，求的度数；

（2）求证：；

（3）若，，，求的长．

【题目】如图，BC是⊙O的直径，点A在⊙O上，AD⊥BC，垂足为D，＝，BE分别交AD、AC延长线于点F、G．

（1）过点A作直线MN，使得MN∥BG，判断直线MN与⊙O的位置关系，并说理．

（2）若AC＝3，AB＝4，求BG的长．

（3）连接CE，探索线段BD、CD与CE之间的数量关系，并说明理由．

【题目】如图，在平面直角坐标系中，抛物线y=ax2+bx+c（a＜0）与x轴交于A（﹣2，0）、B（4，0）两点，与y轴交于点C，且OC=2OA．

（1）试求抛物线的解析式；

（2）直线y=kx+1（k＞0）与y轴交于点D，与抛物线交于点P，与直线BC交于点M，记m=，试求m的最大值及此时点P的坐标；

（3）在（2）的条件下，点Q是x轴上的一个动点，点N是坐标平面内的一点，是否存在这样的点Q、N，使得以P、D、Q、N四点组成的四边形是矩形？如果存在，请求出点N的坐标；如果不存在，请说明理由．

【题目】已知二次函数（是常数，）的与的部分对应值如下表：

0

2

6

0

6

下列结论：

①；

②当时，函数最小值为；

③若点，点在二次函数图象上，则；

④方程有两个不相等的实数根．

其中，正确结论的序号是__________________．（把所有正确结论的序号都填上）

【题目】如图，等腰的边与正方形的边重合，．从如图所示位置水平向右匀速运动，直到点落在边上．设，运动过程中与正方形的重合部分面积为，则能反映与的函数关系的图象是（ ）

A.B.

C.D.

【题目】如图，一次函数y＝kx+b（k≠0）的图象与反比例函数y＝（m≠0，x＞0）的图象在第一象限内交于点A，B，且该一次函数的图象与y轴正半轴交于点C，过A，B分别作y轴的垂线，垂足分别为D，E．已知A（1，4），＝．

（1）求m的值和一次函数的解析式；

（2）若点M为反比例函数图象在A，B之间的动点，作射线OM交直线AB于点N，当MN长度最大时，直接写出点M的坐标．

【题目】如图，抛物线与x轴相交于点A（﹣3，0）、点B（1，0），与y轴交于点C（0，3），点D是抛物线上一动点，联结OD交线段AC于点E．

（1）求这条抛物线的解析式，并写出顶点坐标；

（2）求∠ACB的正切值；

（3）当△AOE与△ABC相似时，求点D的坐标．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网