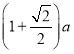ЬтФПФкШн
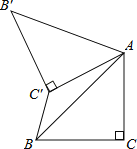
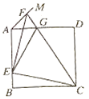
ЁОЬтФПЁПЃЈ1ЃЉШчЭМ1ЃЌEЪЧе§ЗНаЮABCDБпABЩЯЕФвЛЕуЃЌСЌНгBDЁЂDEЃЌНЋЁЯBDEШЦЕуDФцЪБеыа§зЊ90ЁуЃЌа§зЊКѓНЧЕФСНБпЗжБ№гыЩфЯпBCНЛгкЕуFКЭЕуGЃЎ

ЂйЯпЖЮDBКЭDGЕФЪ§СПЙиЯЕЪЧЁЁ ЁЁЃЛ
ЂкаДГіЯпЖЮBEЃЌBFКЭDBжЎМфЕФЪ§СПЙиЯЕЃЎ
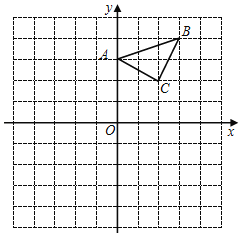
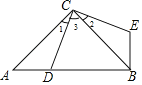
ЃЈ2ЃЉЕБЫФБпаЮABCDЮЊСтаЮЃЌЁЯADCЃН60ЁуЃЌЕуEЪЧСтаЮABCDБпABЫљдкжБЯпЩЯЕФвЛЕуЃЌСЌНгBDЁЂDEЃЌНЋЁЯBDEШЦЕуDФцЪБеыа§зЊ120ЁуЃЌа§зЊКѓНЧЕФСНБпЗжБ№гыЩфЯпBCНЛгкЕуFКЭЕуGЃЎ
ЂйШчЭМ2ЃЌЕуEдкЯпЖЮABЩЯЪБЃЌЧыЬНОПЯпЖЮBEЁЂBFКЭBDжЎМфЕФЪ§СПЙиЯЕЃЌаДГіНсТлВЂИјГіжЄУїЃЛ
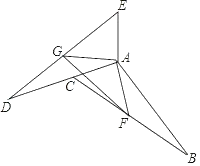
ЂкШчЭМ3ЃЌЕуEдкЯпЖЮABЕФбгГЄЯпЩЯЪБЃЌDEНЛЩфЯпBCгкЕуMЃЌШєBEЃН1ЃЌABЃН2ЃЌжБНгаДГіЯпЖЮGMЕФГЄЖШЃЎ
ЁОД№АИЁПЃЈ1ЃЉЂйDBЃНDGЃЛЂкBF+BEЃН![]() BDЃЛЃЈ2ЃЉЂйBF+BEЃН
BDЃЛЃЈ2ЃЉЂйBF+BEЃН![]() BDЃЌРэгЩМћНтЮіЃЛЂкGMЃН
BDЃЌРэгЩМћНтЮіЃЛЂкGMЃН![]() .
.
ЁОНтЮіЁП
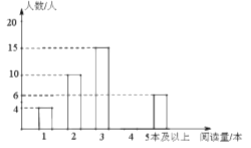
ЃЈ1ЃЉЂйИљОна§зЊЕФаджЪНтД№МДПЩЃЛ
ЂкИљОне§ЗНаЮЕФаджЪКЭШЋЕШШ§НЧаЮЕФХаЖЈКЭаджЪНтД№МДПЩЃЛ
ЃЈ2ЃЉЂйИљОнСтаЮЕФаджЪКЭШЋЕШШ§НЧаЮЕФХаЖЈКЭаджЪНтД№МДПЩЃЛ
ЂкзїИЈжњЯпЃЌМЦЫуBDКЭBFЕФГЄЃЌИљОнЦНааЯпЗжЯпЖЮГЩБШР§ЖЈРэПЩЕУBMЕФГЄЃЌИљОнЯпЖЮЕФВюПЩЕУНсТлЃЎ
НтЃКЃЈ1ЃЉЂйDBЃНDGЃЌ
РэгЩЪЧЃК
ЁпЁЯDBEШЦЕуBФцЪБеыа§зЊ90ЁуЃЌШчЭМ1ЃЌ
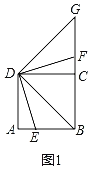
гЩа§зЊПЩжЊЃЌЁЯBDEЃНЁЯFDGЃЌЁЯBDGЃН90ЁуЃЌ
ЁпЫФБпаЮABCDЪЧе§ЗНаЮЃЌ
ЁрЁЯCBDЃН45ЁуЃЌ
ЁрЁЯGЃН45ЁуЃЌ
ЁрЁЯGЃНЁЯCBDЃН45ЁуЃЌ
ЁрDBЃНDGЃЛ
ЙЪД№АИЮЊЃКDBЃНDGЃЛ
ЂкBF+BEЃН![]() BDЃЌРэгЩШчЯТЃК
BDЃЌРэгЩШчЯТЃК
гЩЂйжЊЃКЁЯFDGЃНЁЯEDBЃЌЁЯGЃНЁЯDBEЃН45ЁуЃЌBDЃНDGЃЌ
ЁрЁїFDGЁеЁїEDBЃЈASAЃЉЃЌ
ЁрBEЃНFGЃЌ
ЁрBF+FGЃНBF+BEЃНBC+CGЃЌ
RtЁїDCGжаЃЌЁпЁЯGЃНЁЯCDGЃН45ЁуЃЌ
ЁрCDЃНCGЃНCBЃЌ
ЁпDGЃНBDЃН![]() BCЃЌ
BCЃЌ
МДBF+BEЃН2BCЃН![]() BDЃЛ
BDЃЛ
ЃЈ2ЃЉЂйШчЭМ2ЃЌBF+BEЃН![]() BDЃЌ
BDЃЌ
РэгЩШчЯТЃКдкСтаЮABCDжаЃЌЁЯADBЃНЁЯCDBЃН![]()
![]() ЁЯADCЃН
ЁЯADCЃН![]() ЁС60ЁуЃН30ЁуЃЌ
ЁС60ЁуЃН30ЁуЃЌ
гЩа§зЊ120ЁуЕУЁЯEDFЃНЁЯBDGЃН120ЁуЃЌЁЯEDBЃНЁЯFDGЃЌ
дкЁїDBGжаЃЌЁЯGЃН180ЁуЉ120ЁуЉ30ЁуЃН30ЁуЃЌ
ЁрЁЯDBGЃНЁЯGЃН30ЁуЃЌ
ЁрDBЃНDGЃЌ
ЁрЁїEDBЁеЁїFDGЃЈASAЃЉЃЌ
ЁрBEЃНFGЃЌ
ЁрBF+BEЃНBF+FGЃНBGЃЌ
Й§ЕуDзїDMЁЭBGгкЕуMЃЌШчЭМ2ЃЌ
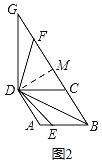
ЁпBDЃНDGЃЌ
ЁрBGЃН2BMЃЌ
дкRtЁїBMDжаЃЌЁЯDBMЃН30ЁуЃЌ
ЁрBDЃН2DMЃЎ
ЩшDMЃНaЃЌдђBDЃН2aЃЌ
BMЃН![]() aЃЌ
aЃЌ
ЁрBGЃН2![]() aЃЌ
aЃЌ
Ёр![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрBGЃН![]() BDЃЌ
BDЃЌ
ЁрBF+BEЃНBGЃН![]() BDЃЛ
BDЃЛ
ЂкЙ§ЕуAзїANЁЭBDгкNЃЌЙ§DзїDPЁЭBGгкPЃЌШчЭМ3ЃЌ
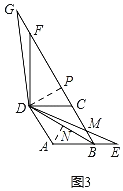
RtЁїABNжаЃЌЁЯABNЃН30ЁуЃЌABЃН2ЃЌ
ЁрANЃН1ЃЌBNЃН![]() ЃЌ
ЃЌ
ЁрBDЃН2BNЃН2![]() ЃЌ
ЃЌ
ЁпDCЁЮBEЃЌ
Ёр![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁпCM+BMЃН2ЃЌ
ЁрBMЃН![]() ЃЌ
ЃЌ
RtЁїBDPжаЃЌЁЯDBPЃН30ЁуЃЌBDЃН2![]() ЃЌ
ЃЌ
ЁрBPЃН3ЃЌ
гЩа§зЊЕУЃКBDЃНBFЃЌ
ЁрBFЃН2BPЃН6ЃЌ
ЁрGMЃНBGЉBMЃН6+1Љ![]() ЃН
ЃН![]()

 ПкЫуаЁзДдЊПкЫуЫйЫуЬьЬьСЗЯЕСаД№АИ
ПкЫуаЁзДдЊПкЫуЫйЫуЬьЬьСЗЯЕСаД№АИ