题目内容
【题目】如图,正方形ABCD的边长为a,点E在边AB上运动(不与点A,B重合),∠DAM=45°,点F在射线AM上,且![]() ,CF与AD相交于点G,连接EC,EF,EG,则下列结论:①∠ECF=45°;②
,CF与AD相交于点G,连接EC,EF,EG,则下列结论:①∠ECF=45°;②![]() 的周长为
的周长为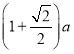 ;③
;③![]() ;④
;④![]() 的面积的最大值
的面积的最大值![]() .其中正确的结论是____.(填写所有正确结论的序号)
.其中正确的结论是____.(填写所有正确结论的序号)
【答案】①④
【解析】
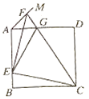
①正确.如图1中,在BC上截取BH=BE,连接EH.证明△FAE≌△EHC(SAS),即可解决问题;
②③错误.如图2中,延长AD到H,使得DH=BE,则△CBE≌△CDH(SAS),再证明△GCE≌△GCH(SAS),即可解决问题;
④正确.设BE=x,则AE=a-x,AF=![]() ,构建二次函数,利用二次函数的性质解决最值问题.
,构建二次函数,利用二次函数的性质解决最值问题.
解:如图1,在BC上截取BH=BE,连接EH.
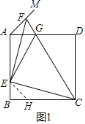
∵BE=BH,∠EBH=90°,
∴EH=![]() BE,∵AF=
BE,∵AF=![]() BE,∴AF=EH,
BE,∴AF=EH,
∵∠DAM=∠EHB=45°,∠BAD=90°,
∴∠FAE=∠EHC=135°,
∵BA=BC,BE=BH,
∴AE=HC,∴△FAE≌△EHC(SAS),
∴EF=EC,∠AEF=∠ECH,
∵∠ECH+∠CEB=90°,∴∠AEF+∠CEB=90°,∴∠FEC=90°,
∴∠ECF=∠EFC=45°,故①正确,
如图2中,延长AD到H,使得DH=BE,则△CBE≌△CDH(SAS),
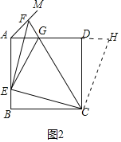
∴∠ECB=∠DCH,∴∠ECH=∠BCD=90°,∴∠ECG=∠GCH=45°,
∵CG=CG,CE=CH,∴△GCE≌△GCH(SAS),∴EG=GH,
∵GH=DG+DH,DH=BE,
∴EG=BE+DG,故③错误,
∴△AEG的周长=AE+EG+AG=AG+GH=AD+DH+AE=AE+EB+AD=AB+AD=2a,故②错误,
设BE=x,则AE=a-x,AF=![]() ,
,
∴∴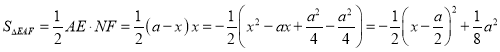 ,
,
∴当![]() 时,
时,![]() 的面积有最大值,最大值是
的面积有最大值,最大值是![]() ,④正确;
,④正确;
故答案为:①④.

 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案