Question

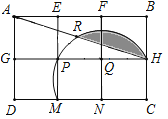
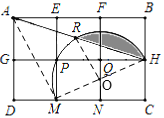
【题目】如图，用6个小正方形构造如图所示的网格图（每个小正方形的边长均为2），设经过图中M、P、H三点的圆弧与AH交于R，则图中阴影部分面积（ ）

A.π﹣B.π﹣5C.2π﹣5D.3π﹣2

Answer 1

【答案】A

【解析】

如图，连接MH交FN于O，连接AM、OR，根据垂径定理可得圆心在FN所在直线上，根据圆周角定理可得MH为直径，即可得出点O为圆心，利用SAS可证明△ADM≌△MCH，可得AM=MH，进而可得∠AMH=90°，可得∠MHA=45°，根据等腰三角形的性质可得∠ROH=90°，利用勾股定理可求出MH的长，即可得OH的长，利用S阴影=S扇形ORH-S△ORH即可得答案.

如图，连接MH交FN于O，连接AM、OR，

∵PQ=HQ，FN⊥PH，

∴圆心在FN所在直线上，

∵∠MPH=90°，点M、P、H在圆上，

∴MN为直径，

∴点O为圆心，

∵AD=MC，∠D=∠C，DM=CH，

∴△ADM≌△MCH，

∴AM=MH，∠DAM=∠HMC，

∵∠DAM+∠AMD=90°，

∴∠HMC+∠AMD=90°，

∴∠AMH=90°，

∴∠MHA=45°，

∵OH=OR，

∴ROH=90°，

∵MH==，

∴OH=MH=，

∴S阴影=S扇形ORH-S△ORH=-=π﹣.

故选A.