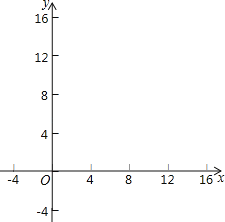��Ŀ����
����Ŀ����ͼ����ABC��ƽ��ֱ������ϵ�У�������������ֱ�ΪA��0��3����B��3��4����C��2��2����������ÿ�������εı߳���1����λ���ȣ���
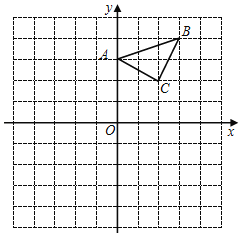
��1���Ե�BΪλ�����ģ��������ڻ�����A��BC����ʹ��A��BC������ABCλ�ƣ���λ�Ʊ�Ϊ2��1�����C����������______��
��2����A��BC���������_______ƽ����λ��
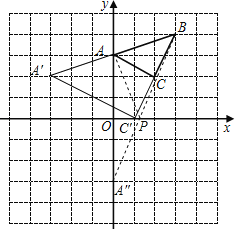
��3����x�����ҳ���P��ʹ�õ�P��B���A����֮����С����ֱ��д��P������꣮
���𰸡���1����1��0������2��10����3����![]() ��0����
��0����
��������
��1������λ��ͼ�ε����ʵó���Ӧ��λ�ã����ɵó��𰸣���2�����ù��ɶ����涨���ɵ���A��BC����ֱ�������Σ����������������ʽ�����A��BC��������ɣ���3����A����y��ĶԳƵ�A��������A��B����x���ڵ�P�����ݶԳ����ʿɵ�A��B��ΪPA+PB����Сֵ������A����B������ɵ�ֱ��A��B�Ľ���ʽ����y=0���ɵ�P������.
��1����ͼ��ʾ��C����1��0����
�ʴ�Ϊ����1��0����
��2����A��B2=62+22=40��A��C��2=42+22=20��C��B2=42+22=20��
��A��B2=A��C��2+C��B2��
����A��BC����ֱ�������Σ�
����A��BC��������ǣ�![]() ��2
��2![]() ��2
��2![]() ��10ƽ����λ��
��10ƽ����λ��
�ʴ�Ϊ��10
��3����A����y��ĶԳƵ�A��������A��B����x���ڵ�P��
��PA=PA����
��PA��+PB=PA+PB=BA������ΪPA+PB����Сֵ��
��A��Bֱ�߽���ʽΪ��y��kx+b��
�ѣ�3��4������0����3��������ã�![]() ��
��
��ã�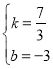 ��
��
��A��Bֱ�߽���ʽΪ��y��![]() x��3��
x��3��
��y��0ʱ��x��![]() ��
��
��P��![]() ��0����
��0����

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�