题目内容
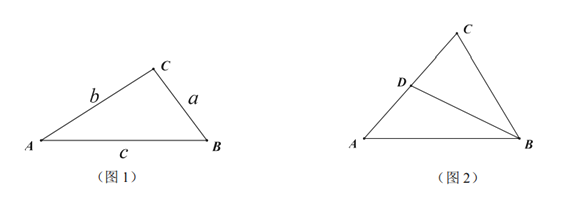
【题目】如图1,![]() 的
的![]() 所对边分别是
所对边分别是![]() ,且
,且![]() ,若满足
,若满足![]() ,则称
,则称![]() 为奇异三角形,例如等边三角形就是奇异三角形.
为奇异三角形,例如等边三角形就是奇异三角形.
(1)若![]() ,判断
,判断![]() 是否为奇异三角形,并说明理由;
是否为奇异三角形,并说明理由;
(2)若![]() ,
,![]() ,求
,求![]() 的长;
的长;
(3)如图2,在奇异三角形![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边上的中点,连结
边上的中点,连结![]() ,
,![]() 将
将![]() 分割成2个三角形,其中
分割成2个三角形,其中![]() 是奇异三角形,
是奇异三角形,![]() 是以
是以![]() 为底的等腰三角形,求
为底的等腰三角形,求![]() 的长.
的长.
【答案】(1)是,理由见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据奇异三角形的概念直接进行判断即可.
(2)根据勾股定理以及奇异三角形的概念直接列式进行计算即可.
(3)根据△ABC是奇异三角形,且b=2,得到![]() ,由题知:AD=CD=1,且BC=BD=a,根据△ADB是奇异三角形,则
,由题知:AD=CD=1,且BC=BD=a,根据△ADB是奇异三角形,则![]() 或
或![]() ,分别求解即可.
,分别求解即可.
(1)∵![]() ,
, ![]() ,
,![]()
∴![]() ,
,![]()
∴![]()
即△ABC是奇异三角形.
(2)∵∠C=90°,![]()
∴![]()
∵![]()
∴![]()
![]() ,
,
∴![]()
解得:![]() .
.
(3)∵△ABC是奇异三角形,且b=2
∴![]()
由题知:AD=CD=1,BC=BD=a
∵△ADB是奇异三角形,且![]() ,
,![]()
∴![]() 或
或![]()
当![]() 时,
时,![]()
当![]() 时,与
时,与![]() 矛盾,不合题意.
矛盾,不合题意.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目