题目内容
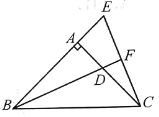
【题目】如图,平面上有射线AP和点B,C,请用尺规按下列要求作图:
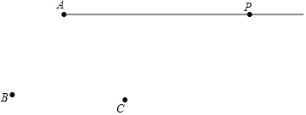
(1)连接AB,并在射线AP上截取AD=AB;
(2)连接BC、BD,并延长BC到E,使BE=BD.
(3)在(2)的基础上,取BE中点F,若BD=6,BC=4,求CF的值.
【答案】(1)见解析;(2)见解析;(3)CF的值为1
【解析】
(1)连接AB,并在射线AP上截取AD=ABJ即可;
(2)连接BC、BD,并延长BC到E,使BE=BD即可;
(3)在(2)的基础上,取BE中点F,根据BD=6,BC=4,即可求CF的值.
解:如图所示,
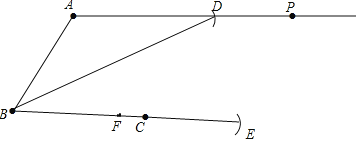
(1)连接AB,并在射线AP上截取AD=AB;
(2)连接BC、BD,并延长BC到E,使BE=BD.
(3)在(2)的基础上,
∵BE=BD=6,BC=4,
∴CE=BE﹣BC=2
∵F是BE的中点,
∴BF=![]() =
=![]() =3
=3
∴CF=BC﹣BF=4﹣3=1.
答:CF的值为1.

练习册系列答案
相关题目