Question

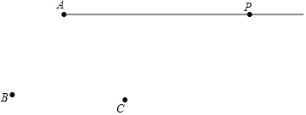
【题目】如图，在数轴上每相邻两点间的距离为一个单位长度．点A、B、C、D对应的数分别是a、b、c、d，且d﹣3a＝20．

（1）a＝　 　，b＝　 　，c＝　 　．

（2）点A以2个单位/秒的速度沿着数轴的正方向运动，1秒后点B以4个单位/秒的速度也沿着数轴的正方向运动．当点B到达D点处立刻返回，返回时，点A与点B在数轴的某点处相遇，求这个点对应的数．

（3）如果A、C两点分别以2个单位/秒和3个单位/秒的速度同时向数轴的负方向运动，同时，点B从图上的位置出发向数轴的正方向以1个单位/秒的速度运动，当满足AB+AC＝AD时，点A对应的数是多少？

Answer 1

【答案】（1）﹣6，﹣8，﹣3；（2）A、B相遇时，这个点对应的数为 ；（3）点A对应的数是或﹣12．

【解析】

（1）由数轴可知d=a+8，结合d-3a=20可求a的值，进而可求出b、c的值；

（2）先求出BD=10，B点运动到D点需要时间为2.5秒，此时A点运动到-6+2×3.5=1，可得AB距离为1，求出AB相遇时间为秒，即可求相遇位置；

（3）设运动时间为t秒，A点运动t秒后对应的数为-6-2t，C点运动t秒后对应的数为-3-3t，B点运动t秒后对应的数为-8+t，由AB+AC=AD，可得|2-3t|+|t-3|=|4+t|，分三种情况去掉绝对值分别求解：当0≤t≤时，2-3t+3-t=4+t，当t≤3时，3t-2+t-3=4+t，当t＞3时，3t-2+3-t=4+t，求出t的值即可求A表示的数．

（1）由数轴可知，d＝a+8，

∵d﹣3a＝20，

∴a+8﹣3a＝20，

∴a＝﹣6，

∴b＝﹣8，c＝﹣3，

故答案为﹣6，﹣8，﹣3；

（2）∵a＝﹣6，

∴d＝2，

∴BD＝10，

B点运动到D点需要时间为2.5秒，此时A点运动到﹣6+2×3.5＝1，

∴AB距离为1，

∴AB相遇时间为＝秒，

此时A点位置为1+＝，

∴A、B相遇时的点对应的数为．

（3）设运动时间为t秒，

A点运动t秒后对应的数为﹣6﹣2t，C点运动t秒后对应的数为﹣3﹣3t，B点运动t秒后对应的数为﹣8+t，

∴AB＝|﹣6﹣2t+8﹣t|＝|2﹣3t|，AC＝|﹣6﹣2t+3+3t|＝|t﹣3|，AD＝|2+6+2t|＝|8+2t|，

∵AB+AC＝AD，

∴|2﹣3t|+|t﹣3|＝|4+t|，

①当B与A相遇时，t+2t=2，解得t=,

∴当0≤t≤时，

2﹣3t+3﹣t＝4+t，

∴t＝，

②当A与C相遇时，

3t-2t=3，

解得t=3，

∴当≤3时，

3t﹣2+t﹣3＝4+t，

∴t＝3，

③当t＞3时，3t﹣2+3﹣t＝4+t，

∴t＝3，

∴t＝或t＝3，

∴A点表示的数是﹣或﹣12．