题目内容
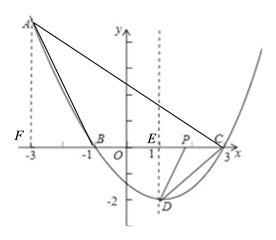
【题目】已知二次函数![]() 的图象经过点A(﹣3,6)、B(m,0)、C(3,0),并且m<3,D为抛物线的顶点.
的图象经过点A(﹣3,6)、B(m,0)、C(3,0),并且m<3,D为抛物线的顶点.
(1)求b,c,m的值;
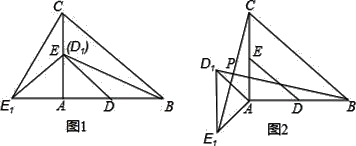
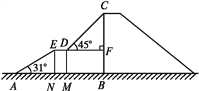
(2)设点P是线段OC上一点,点O是坐标原点,且满足∠PDC=∠BAC,求点P的坐标.
【答案】(1)b=﹣1,c=﹣![]() ,m=﹣1;(2)P点坐标为(
,m=﹣1;(2)P点坐标为(![]() ,0).
,0).
【解析】试题分析:
(1)把点A、C的坐标代入![]() 列出关于b、c的二元一次方程组,解方程组即可得到b、c的值;再把所得b、c的值和点B的坐标代入
列出关于b、c的二元一次方程组,解方程组即可得到b、c的值;再把所得b、c的值和点B的坐标代入![]() 即可求得m的值;
即可求得m的值;
(2)由![]() 可得抛物线顶点的坐标为D(1,-2),对称轴为直线
可得抛物线顶点的坐标为D(1,-2),对称轴为直线![]() ;设抛物线对称轴和x轴交于点E,过点A(-3,6)作AF⊥x轴于点F,则易证△AFC和△DEC都是等腰直角三角形,从而可得∠PCD=∠ACB结合∠PDC=∠BAC,
;设抛物线对称轴和x轴交于点E,过点A(-3,6)作AF⊥x轴于点F,则易证△AFC和△DEC都是等腰直角三角形,从而可得∠PCD=∠ACB结合∠PDC=∠BAC,
△ABC∽△DPC,由此可解出PC的值,即可求得OP的值,从而可得点P的坐标.
试题解析:
(1)把A(﹣3,6)、C(3,0)代入解析式得: ![]() ,解得
,解得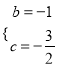 ,
,
∴抛物线的解析式为:y=![]() x2﹣x﹣
x2﹣x﹣![]() ,
,
当y=0,则![]() x2﹣x﹣
x2﹣x﹣![]() =0,解得,x1=3,x2=﹣1,
=0,解得,x1=3,x2=﹣1,
∵m<3,
∴m=﹣1,
∴ b=﹣1,c=﹣![]() ,m=﹣1;
,m=﹣1;
(2)由![]() 可得抛物线顶点的坐标为D(1,-2),对称轴为直线
可得抛物线顶点的坐标为D(1,-2),对称轴为直线![]() ,
,
设抛物线对称轴和x轴交于点E,过点A(-3,6)作AF⊥x轴于点F,
则DE=2,DC=OC-OD=2,AF=6,FC=3-(-3)=6,
∴DE=DC,AF=FC,
∴△AFC和△DEC都是等腰直角三角形,
∴∠PCD=∠ACB=45°,AC=![]() ,DC=
,DC=![]() ,
,
∵∠PDC=∠BAC,
∴△ABC∽△DPC,
∴![]() ,
,
∴BCDC=ACPC,即![]() ,
,
解得:PC=![]() ,则OP=
,则OP=![]() ,
,
所以P点坐标为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目