题目内容
【题目】如图1, ![]() 与
与 ![]() 为等腰直角三角形,
为等腰直角三角形, ![]() 与
与 ![]() 重合,
重合, ![]() ,
, ![]() .固定
.固定 ![]() ,将
,将 ![]() 绕点
绕点 ![]() 顺时针旋转,当
顺时针旋转,当 ![]() 边与
边与 ![]() 边重合时,旋转终止.现不考虑旋转开始和结束时重合的情况,设
边重合时,旋转终止.现不考虑旋转开始和结束时重合的情况,设 ![]() (或它们的延长线)分别交
(或它们的延长线)分别交 ![]() (或它们的延长线)于点
(或它们的延长线)于点 ![]() ,如图2.
,如图2.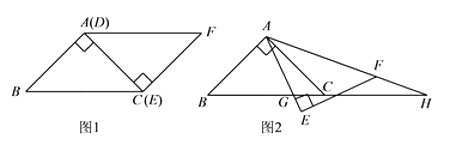
(1)证明: ![]() ;
;
(2)当 ![]() 为何值时,
为何值时, ![]() 是等腰三角形?
是等腰三角形?
【答案】
(1)证明:∵△ABC与△EFD为等腰直角三角形,AC与DE重合,
∴∠B=∠EDF=45°
在△AGC和△HAB中
∵∠ACG=∠B=45°,
∠HAB=∠BAG+∠GAH =∠BAG+45°=∠CGA
∴△AGC∽△HAB
(2)解:①当∠GAH=45是等腰三角形的底角时,
如图可知: ![]() ;
;

②当∠GAH=45是等腰三角形的顶角时,如图:

在△HGA和△AGC中,
∵∠AGH=∠CGA,∠GAH=∠C=45,
∴△HGA∽△AGC,∵AG=AH,
∴ ![]()
③如图,G与B重合时,符合要求,

此时CG=BC= ![]()
∴当 ![]() 或
或 ![]() 或
或 ![]() 时,
时,
△AGH是等腰三角形
【解析】第1小题,根据等腰三角形的性质可得∠B=∠EDF=45°,由有两个角对应相等的两个三角形相似可证△AGC∽△HAB;第2小题,分三种情况,①当∠GAH=45是等腰三角形的底角时;②当∠GAH=45是等腰三角形的顶角时;③G与B重合时。

练习册系列答案
相关题目